
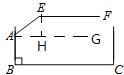
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. B.
B. C.
C. D.
D.
【答案】A
【解析】
试题分析:过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AEsin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.
解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,
则∠EHG=∠HEF=90°,
∵∠AEF=143°,
∴∠AEH=∠AEF﹣∠HEF=53°,
∠EAH=37°,
在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.2米,
∴EH=AEsin∠EAH≈1.2×0.60=0.72(米),
∵AB=1.2米,
∴AB+EH≈1.2+0.72=1.92≈1.9米.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD边AD上的一个动点,且与点A、点D不重合,连结BE、CE,过点B作BF∥CE,过点C作CF∥BE,交点为F点,连接AF、DF分别交BC于点G、H,则下列结论错误的是( )
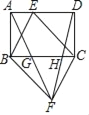
A. GH=![]() BC B. S△BGF+S△CHF=
BC B. S△BGF+S△CHF=![]() S△BCF
S△BCF
C. S四边形BFCE=ABAD D. 当点E为AD中点时,四边形BECF为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,他们的运动时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由
(2)判断此时线段PC和线段PQ的关系,并说明理由。
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变,设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ADE中,∠DAE=90°,C是边AE上任意一点(点C与点A、E不重合),以AC为一直角边在Rt△ADE的外部作Rt△ABC,∠BAC=90°,连接BE、CD.
(1)在图1中,若AC=AB,AE=AD,现将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图2,那么线段BE.CD之间有怎样的关系,写出结论,并说明理由;
(2)在图1中,若CA=3,AB=5,AE=10,AD=6,将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图3,连接BD、CE.
①求证:△ABE∽△ACD;
②计算:BD2+CE2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和哥哥一起骑自行车从家里出发到昌南湖游玩,从家出发0.5小时后到达陶溪川,游玩一段时间后按原速前往昌南湖.小明离家80分钟后,爸爸驾车沿相同路线前往昌南湖,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知爸爸驾车的速度是小明骑车速度的3倍.
(1)小明骑车的速度为_____km/h,爸爸驾车的速度为_____km/h.
(2)小明从家到陶溪川的路程y与时间x的函数关系式为_____,他从陶溪川到昌南湖的路程y与时间x的函数关系式为______,爸爸从家到昌南湖的路程,与时间x的函数关系式为______.
(3)小明从家出发多少小时后被爸爸追上?此时离家多远?
(4)如果小明比爸爸晚10分钟到达昌南湖,那么昌南湖离家有多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
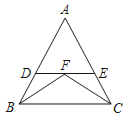
【题目】如图,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,下列结论正确的是( )
①BD=CE②△BDF,△CEF都是等腰三角形③BD+CE=DE④△ADE的周长为AB+AC.
A.①②B.③④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在 Rt△ABC 中,∠ACB=90°,AC=BC,D 是 BC 上的一点,过点 D 作 DE⊥AB,垂足为点 E,F 为 AD 的中点,连接 CF、EF.

(1)猜想CF与EF的关系,并说明理由;
(2)如图2,连接BF,若∠AEF=30°,求∠BFE 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com