
【题目】如图,点E是矩形ABCD边AD上的一个动点,且与点A、点D不重合,连结BE、CE,过点B作BF∥CE,过点C作CF∥BE,交点为F点,连接AF、DF分别交BC于点G、H,则下列结论错误的是( )
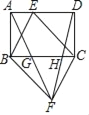
A. GH=![]() BC B. S△BGF+S△CHF=
BC B. S△BGF+S△CHF=![]() S△BCF
S△BCF
C. S四边形BFCE=ABAD D. 当点E为AD中点时,四边形BECF为菱形
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个面积为150平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙,墙长为18米,另三边用篱笆围成,如篱笆长度为35米,且要求用完。求鸡场的长与宽各是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形
(1) 如图1,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF,连接EF,猜想线段AB、DB、AF之间的数量关系
(2) 点E在线段BA的延长线上,其他条件与(1)中的一致,请在图2上将图形补充完整,并猜想证明线段AB、DB、AF之间的数量关系

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为等边三角形,
为等边三角形,![]() 点坐标为
点坐标为![]() ,点
,点![]() 为
为![]() 轴上位于
轴上位于![]() 点上方的一个动点,以
点上方的一个动点,以![]() 为边向
为边向![]() 的右侧作等边
的右侧作等边![]() ,连接
,连接![]() ,并延长
,并延长![]() 交
交![]() 轴于点
轴于点![]() .
.

(1)求证:![]() ;
;
(2)当点![]() 在运动时,
在运动时,![]() 是否平分
是否平分![]() ?请说明理由;
?请说明理由;
(3)当点![]() 在运动时,在
在运动时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,请求出点
为等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.
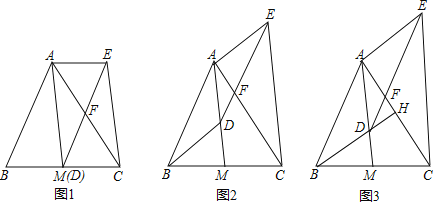
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM
①求∠CAM的度数;
②当FH=![]() , DM=4时,求DH的长.
, DM=4时,求DH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com