
【题目】如图,在平面直角坐标系中,![]() 为等边三角形,
为等边三角形,![]() 点坐标为
点坐标为![]() ,点
,点![]() 为
为![]() 轴上位于
轴上位于![]() 点上方的一个动点,以
点上方的一个动点,以![]() 为边向
为边向![]() 的右侧作等边
的右侧作等边![]() ,连接
,连接![]() ,并延长
,并延长![]() 交
交![]() 轴于点
轴于点![]() .
.

(1)求证:![]() ;
;
(2)当点![]() 在运动时,
在运动时,![]() 是否平分
是否平分![]() ?请说明理由;
?请说明理由;
(3)当点![]() 在运动时,在
在运动时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,请求出点
为等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)见解析(2)![]() 平分
平分![]() ,理由见解析(3)存在,Q(0,3),(0,1).
,理由见解析(3)存在,Q(0,3),(0,1).
【解析】
(1)根据等边三角形性质得出OP=AP,BP=PC,∠APO=∠CPB=60°,求出∠OPB=∠APC,证出△PBO≌△PCA即可;
(2)由(1)知∠POB=∠PAC=60゜,得到∠PAC=∠OAP=60゜,即可得到![]() 平分
平分![]() ;
;
(3)①当AQ=AE=2时,△AEQ为等腰三角形,点Q在y轴的正半轴上,求得OQ=AE+AO=3,②当AQ=AE=2时,△AEQ为等腰三角形,点Q在y轴的负半轴上,求得OQ=AQAO=1,③当EQ=AE=2时,△AEQ为等腰三角形,x轴是AQ的垂直平分线,求得OQ=AO=1,即可得到结论.

(1)证明:∵△BPC和△AOP是等边三角形,
∴OP=AP,BP=PC,∠APO=∠CPB=60°,
∴∠APO+∠APB=∠BPC+∠APB,
即∠OPB=∠APC,
在△PBO和△PCA中,
 ,
,
∴△PBO≌△PCA (SAS)
∴OB=AC.
(2)![]() 平分
平分![]() ,理由如下:
,理由如下:
由(1)知∠POB=∠PAC=60゜,
∴∠PAC=∠OAP=60゜,
∴![]() 平分
平分![]() ;
;
(3)解:存在,
∵AE=2AO=2,
∴①当AQ=AE=2时,△AEQ为等腰三角形,点Q在y轴的正半轴上,
∴OQ=AE+AO=3,
∴Q(0,3),
②当AQ=AE=2时,△AEQ为等腰三角形,点Q在y轴的负半轴上,
∴OQ=AQAO=1,
∴Q(0,1),
③当EQ=AE=2时,△AEQ为等腰三角形,x轴是AQ的垂直平分线,
∴OQ=AO=1,
∴Q(0,1).
综上所述:在y轴上存在点Q,使得△AEQ为等腰三角形,Q(0,3),(0,1).


科目:初中数学 来源: 题型:
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将每件进价![]() 元的某种商品按每件
元的某种商品按每件![]() 元出售,一天可销出约
元出售,一天可销出约![]() 件,该店想通过降低售价,增加销售量的办法来提高利润,经过市场调查,发现这种商品单价每降低
件,该店想通过降低售价,增加销售量的办法来提高利润,经过市场调查,发现这种商品单价每降低![]() 元,其销售量可增加约
元,其销售量可增加约![]() 件.
件.
![]() 将这种商品每件的售价降低多少时,能使商店的销售利润为
将这种商品每件的售价降低多少时,能使商店的销售利润为![]() 元?
元?
![]() 这种商品的售价降低多少时,才能使商店的销售利润最大?最大利润是多少?
这种商品的售价降低多少时,才能使商店的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知排球场的长度OD为18 m,位于球场中线处球网的高度AB为2.4 m,一队员站在点O处发球,排球从点O的正上方1.6 m的C点向正前方飞出,当排球运行至离点O的水平距离OE为6 m时,到达最高点G建立如图所示的平面直角坐标系
(1) 当球上升的最大高度为3.4 m时,对方距离球网0.4 m的点F处有一队员,他起跳后的最大高度为3.1 m,问这次她是否可以拦网成功?请通过计算说明
(2) 若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD边AD上的一个动点,且与点A、点D不重合,连结BE、CE,过点B作BF∥CE,过点C作CF∥BE,交点为F点,连接AF、DF分别交BC于点G、H,则下列结论错误的是( )
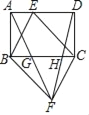
A. GH=![]() BC B. S△BGF+S△CHF=
BC B. S△BGF+S△CHF=![]() S△BCF
S△BCF
C. S四边形BFCE=ABAD D. 当点E为AD中点时,四边形BECF为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,他们的运动时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由
(2)判断此时线段PC和线段PQ的关系,并说明理由。
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变,设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分20分,题b、题c满分均为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,在这个班的平均成绩是__分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com