
ЁОЬтФПЁПШчЭМЃЌвбжЊХХЧђГЁЕФГЄЖШODЮЊ18 mЃЌЮЛгкЧђГЁжаЯпДІЧђЭјЕФИпЖШABЮЊ2.4 mЃЌвЛЖгдБеОдкЕуOДІЗЂЧђЃЌХХЧђДгЕуOЕФе§ЩЯЗН1.6 mЕФCЕуЯђе§ЧАЗНЗЩГіЃЌЕБХХЧђдЫаажСРыЕуOЕФЫЎЦНОрРыOEЮЊ6 mЪБЃЌЕНДязюИпЕуGНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕ
(1) ЕБЧђЩЯЩ§ЕФзюДѓИпЖШЮЊ3.4 mЪБЃЌЖдЗНОрРыЧђЭј0.4 mЕФЕуFДІгавЛЖгдБЃЌЫћЦ№ЬјКѓЕФзюДѓИпЖШЮЊ3.1 mЃЌЮЪетДЮЫ§ЪЧЗёПЩвдРЙЭјГЩЙІЃПЧыЭЈЙ§МЦЫуЫЕУї
(2) ШєЖгдБЗЂЧђМШвЊЙ§ЧђЭјЃЌгжВЛГіБпНчЃЌЮЪХХЧђЗЩааЕФзюДѓИпЖШhЕФШЁжЕЗЖЮЇЪЧЖрЩйЃПЃЈХХЧђбЙЯпЪєгкУЛГіНчЃЉ

ЁОД№АИЁПЃЈ1ЃЉПЩвдРЙЭјГЩЙІЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉhЁн3.025
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнДЫЪБХзЮяЯпЖЅЕузјБъЮЊЃЈ6ЃЌ3.4ЃЉЃЌЩшНтЮіЪНЮЊy=aЃЈxЉ6ЃЉ2+3.4ЃЌдйНЋЕуCзјБъДњШыМДПЩЧѓЕУЃЛгЩНтЮіЪНЧѓЕУx=9.4ЪБyЕФжЕЃЌгыЫћЦ№ЬјКѓЕФзюДѓИпЖШЮЊ3.1УзБШНЯМДПЩЕУЃЛ
ЃЈ2ЃЉЩшХзЮяЯпНтЮіЪНЮЊy=aЃЈxЉ6ЃЉ2+hЃЌНЋЕуCзјБъДњШыЕУЕНгУhБэЪОaЕФЪНзгЃЌдйИљОнЧђМШвЊЙ§ЧђЭјЃЌгжВЛГіБпНчМДx=9ЪБЃЌyЃО2.4Чвx=18ЪБЃЌyЁм0ЕУГіЙигкhЕФВЛЕШЪНзщЃЌНтжЎМДПЩЕУЃЎ
ЃЈ1ЃЉИљОнЬтвтжЊДЫЪБХзЮяЯпЕФЖЅЕуGЕФзјБъЮЊЃЈ6ЃЌ3.4ЃЉЃЌ
ЩшХзЮяЯпНтЮіЪНЮЊy=aЃЈxЉ6ЃЉ2+3.4ЃЌ
НЋЕуCЃЈ0ЃЌ1.6ЃЉДњШыЃЌЕУЃК36a+3.4=1.6ЃЌ
НтЕУЃКa=Љ![]() ЃЌ
ЃЌ
ЁрХХЧђЗЩааЕФИпЖШyгыЫЎЦНОрРыxЕФКЏЪ§ЙиЯЕЪНЮЊy=Љ![]() ЃЈxЉ6ЃЉ2+
ЃЈxЉ6ЃЉ2+![]() ЃЛ
ЃЛ
гЩЬтвтЕБx=9.5ЪБЃЌy=Љ![]() ЃЈ9.4Љ6ЃЉ2+
ЃЈ9.4Љ6ЃЉ2+![]() Ёж2.8ЃМ3.1ЃЌ
Ёж2.8ЃМ3.1ЃЌ
ЙЪетДЮЫ§ПЩвдРЙЭјГЩЙІЃЛ
ЃЈ3ЃЉЩшХзЮяЯпНтЮіЪНЮЊy=aЃЈxЉ6ЃЉ2+hЃЌ
НЋЕуCЃЈ0ЃЌ1.6ЃЉДњШыЃЌЕУЃК36a+h=1.6ЃЌМДa=![]() ЃЌ
ЃЌ
ЁрДЫЪБХзЮяЯпНтЮіЪНЮЊy=![]() ЃЈxЉ6ЃЉ2+hЃЌ
ЃЈxЉ6ЃЉ2+hЃЌ
ИљОнЬтвтЃЌЕУЃК ЃЌ
ЃЌ
НтЕУЃКhЁн3.025ЃЌ
Д№ЃКХХЧђЗЩааЕФзюДѓИпЖШhЕФШЁжЕЗЖЮЇЪЧhЁн3.025ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯACBЃН90ЁуЃЌACЃНBCЃЌЕуC(1ЃЌ2)ЁЂA(Ѓ2ЃЌ0)ЃЌдђЕуBЕФзјБъЪЧ__________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЃКвЊНЋвЛПщжБОЖЮЊ![]() ЕФАыдВаЮЬњЦЄМгЙЄГЩвЛИідВжљЕФСНИіЕзУцКЭвЛИідВзЖЕФЕзУцЃЎ
ЕФАыдВаЮЬњЦЄМгЙЄГЩвЛИідВжљЕФСНИіЕзУцКЭвЛИідВзЖЕФЕзУцЃЎ

ВйзїЃК
ЗНАИвЛЃКдкЭМ![]() жаЃЌЩшМЦвЛИідВзЖЕзУцзюДѓЃЌАыдВаЮЬњЦЄЕУвдзюГфЗжРћгУЕФЗНАИЃЈвЊЧѓЃКЛЪОвтЭМЃЉЃЛ
жаЃЌЩшМЦвЛИідВзЖЕзУцзюДѓЃЌАыдВаЮЬњЦЄЕУвдзюГфЗжРћгУЕФЗНАИЃЈвЊЧѓЃКЛЪОвтЭМЃЉЃЛ
ЗНАИЖўЃКдкЭМ![]() жаЃЌЩшМЦвЛИідВжљСНИіЕзУцзюДѓЃЌАыдВаЮЬњЦЄЕУвдзюГфЗжРћгУЕФЗНАИЃЈвЊЧѓЃКЛЪОвтЭМЃЉЃЎ
жаЃЌЩшМЦвЛИідВжљСНИіЕзУцзюДѓЃЌАыдВаЮЬњЦЄЕУвдзюГфЗжРћгУЕФЗНАИЃЈвЊЧѓЃКЛЪОвтЭМЃЉЃЎ
ЬНОПЃК
![]() ЧѓЗНАИвЛжадВзЖЕзУцЕФАыОЖЃЛ
ЧѓЗНАИвЛжадВзЖЕзУцЕФАыОЖЃЛ
![]() ЧѓЗНАИЖўжаАыдВдВаФЮЊ
ЧѓЗНАИЖўжаАыдВдВаФЮЊ![]() ЃЌдВжљСНИіЕзУцдВаФЮЊ
ЃЌдВжљСНИіЕзУцдВаФЮЊ![]() ЁЂ
ЁЂ![]() ЃЌдВзЖЕзУцЕФдВаФЮЊ
ЃЌдВзЖЕзУцЕФдВаФЮЊ![]() ЃЌЪдХаЖЯвд
ЃЌЪдХаЖЯвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЪВУДбљЕФЬиЪтЫФБпаЮЃЌВЂМгвджЄУїЃЎ
ЮЊЖЅЕуЕФЫФБпаЮЪЧЪВУДбљЕФЬиЪтЫФБпаЮЃЌВЂМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЙигкxЕФвЛдЊЖўДЮЗНГЬЃЈxЈC2ЃЉЃЈxЈC3ЃЉ=mгаЪЕЪ§Иљx1ЁЂx2ЃЌЧвx1<x2ЃЌдђЯТСаНсТлжаДэЮѓЕФЪЧ
A. ЕБm=0ЪБЃЌx1=2ЃЌx2=3
B. m>ЈC![]()
C. ЕБm>0ЪБЃЌ2<x1<x2<3
D. ЖўДЮКЏЪ§y=ЃЈxЈCx1ЃЉЃЈxЈCx2ЃЉ+mЕФЭМЯѓгыxжсНЛЕуЕФзјБъЮЊЃЈ2ЃЌ0ЃЉКЭЃЈ3ЃЌ0ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк10ЁС10ЕФе§ЗНаЮЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЮЊ1ЃЌЭјИёжагавЛИіИёЕуЁїABCЃЈМДШ§НЧаЮЕФЖЅЕуЖМдкИёЕуЩЯЃЉЃЎ
ЃЈ1ЃЉдкЭМжазїГіЁїABCЙигкжБЯпlЖдГЦЕФЁїA1B1C1ЃЛЃЈвЊЧѓЃКAгыA1ЃЌBгыB1ЃЌCгыC1ЯрЖдгІЃЉ
ЃЈ2ЃЉдкЃЈ1ЃЉЮЪЕФНсЙћЯТЃЌСЌНгBB1ЃЌCC1ЃЌЧѓЫФБпаЮBB1C1CЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛБп
НЛБп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЩЯЕФЕуЃЌСЌНс
ЩЯЕФЕуЃЌСЌНс![]() ЃЌ
ЃЌ![]() .Шє
.Шє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дђ
дђ![]() ЕФзюаЁжЕЪЧ__________.
ЕФзюаЁжЕЪЧ__________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() жсЩЯЮЛгк
жсЩЯЮЛгк![]() ЕуЩЯЗНЕФвЛИіЖЏЕуЃЌвд
ЕуЩЯЗНЕФвЛИіЖЏЕуЃЌвд![]() ЮЊБпЯђ
ЮЊБпЯђ![]() ЕФгвВрзїЕШБп
ЕФгвВрзїЕШБп![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌВЂбгГЄ
ЃЌВЂбгГЄ![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() .
.

(1)ЧѓжЄЃК![]() ЃЛ
ЃЛ
(2)ЕБЕу![]() дкдЫЖЏЪБЃЌ
дкдЫЖЏЪБЃЌ![]() ЪЧЗёЦНЗж
ЪЧЗёЦНЗж![]() ЃПЧыЫЕУїРэгЩЃЛ
ЃПЧыЫЕУїРэгЩЃЛ
(3)ЕБЕу![]() дкдЫЖЏЪБЃЌдк
дкдЫЖЏЪБЃЌдк![]() жсЩЯЪЧЗёДцдкЕу
жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕу
ЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌACЃНBCЃЌЁЯACBЃН90ЁуЃЌCEгыABЯрНЛгкЕуDЃЌЧвBEЁЭCEЃЌAFЁЭCEЃЌДЙзуЗжБ№ЮЊЕуEЁЂFЃЎ
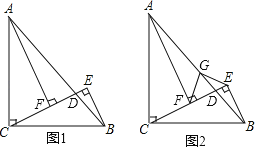
ЃЈ1ЃЉШєAFЃН5ЃЌBEЃН2ЃЌЧѓEFЕФГЄЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌШЁABжаЕуGЃЌСЌНгFCЁЂECЃЌЧыХаЖЯЁїGEFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=x2Љ2xЉ3гыxжсНЛAЁЂBСНЕуЃЈAЕудкBЕузѓВрЃЉЃЌжБЯп1гыХзЮяЯпНЛгкAЁЂCСНЕуЃЌЦфжаCЕуЕФКсзјБъЮЊ2ЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНЕуЕФзјБъМАжБЯпACЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉPЪЧЯпЖЮACЩЯЕФвЛИіЖЏЕуЃЌЙ§PЕузїyжсЕФЦНааЯпНЛХзЮяЯпгкEЕуЃЌЩшPЕуЕФКсзјБъЮЊmЃЎ
ЂйЧѓЯпЖЮPEГЄЖШЕФзюДѓжЕЃЛ
ЂкЕуPНЋЯпЖЮACЗжИюГЩГЄЁЂЖЬСНЬѕЯпЖЮPAЁЂPCЃЌШчЙћНЯГЄЯпЖЮгыACжЎБШЕШгк![]() ЃЌдђГЦPЮЊЯпЖЮACЕФЁАЛЦН№ЗжИюЕуЁБЃЌЧыжБНгаДГіЪЙЕУPЮЊЯпЖЮACЛЦН№ЗжИюЕуЕФmЕФжЕЃЎ
ЃЌдђГЦPЮЊЯпЖЮACЕФЁАЛЦН№ЗжИюЕуЁБЃЌЧыжБНгаДГіЪЙЕУPЮЊЯпЖЮACЛЦН№ЗжИюЕуЕФmЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com