
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线1与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,设P点的横坐标为m.
①求线段PE长度的最大值;
②点P将线段AC分割成长、短两条线段PA、PC,如果较长线段与AC之比等于![]() ,则称P为线段AC的“黄金分割点”,请直接写出使得P为线段AC黄金分割点的m的值.
,则称P为线段AC的“黄金分割点”,请直接写出使得P为线段AC黄金分割点的m的值.

【答案】(1)A(﹣1,0),B(3,0),y=﹣x﹣1;(2)①当x=![]() 时,PE的最大值为
时,PE的最大值为![]() ;②P为线段AC黄金分割点的m的值是
;②P为线段AC黄金分割点的m的值是![]() 或
或![]() .
.
【解析】
(1)令y=0得到关于x的方程,解方程可求得点A和点B的横坐标,将x=2代入抛物线的解析式求得对应的y值可求得点C的纵坐标,设直线AC的解析式为y=kx+b,将点A和点C的坐标代入求得k和b的值即可;
(2)①设P点的横坐标为x(﹣1≤x≤2)则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3),然后得到PE与x的函数关系式,利用二次函数的性质可求得PE的最大值;
②根据黄金分割点,可得答案.
解(1)当y=0时,解得:x1=﹣1或x2=3,∴A(﹣1,0),B(3,0).
将C点的横坐标x=2代入y=x2﹣2x﹣3得:y=﹣3,∴C(2,﹣3).
设直线AC的解析式为y=kx+b,将点A和点C的坐标代入得:![]() ,解得:
,解得:![]() ,∴直线AC的函数解析式是y=﹣x﹣1.
,∴直线AC的函数解析式是y=﹣x﹣1.
(2)①设P点的横坐标为x(﹣1≤x≤2)则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3)
∵P点在E点的上方,∴PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2=﹣(x﹣![]() )2+
)2+![]() ,∴当x=
,∴当x=![]() 时,PE的最大值为
时,PE的最大值为![]() .
.
②设P(m,﹣m﹣1)(﹣1<m<2),A(﹣1,0),C(2,﹣3).
当![]() =
=![]() 时,
时,![]() =
=![]() ,解得:m=
,解得:m=![]() 或m=
或m=![]() <-1(舍去);
<-1(舍去);
当![]() =
=![]() 时,
时,![]() =
=![]() ,解得:m=
,解得:m=![]() 或m=
或m=![]() (舍去).
(舍去).
综上所述:P为线段AC黄金分割点的m的值是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知排球场的长度OD为18 m,位于球场中线处球网的高度AB为2.4 m,一队员站在点O处发球,排球从点O的正上方1.6 m的C点向正前方飞出,当排球运行至离点O的水平距离OE为6 m时,到达最高点G建立如图所示的平面直角坐标系
(1) 当球上升的最大高度为3.4 m时,对方距离球网0.4 m的点F处有一队员,他起跳后的最大高度为3.1 m,问这次她是否可以拦网成功?请通过计算说明
(2) 若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)

查看答案和解析>>
科目:初中数学 来源: 题型:
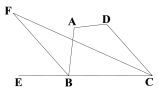
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,下列结论正确的是( )
①BD=CE②△BDF,△CEF都是等腰三角形③BD+CE=DE④△ADE的周长为AB+AC.
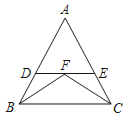
A.①②B.③④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1对应的函数表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求点D,点C的坐标;
(2)求直线l2对应的函数表达式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组![]() 的解.
的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分20分,题b、题c满分均为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,在这个班的平均成绩是__分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子里装有30个除颜色外其它均相同的球,其中红球有m个,白球有3m个,其它均为黄球.现小李从盒子里随机摸出一个球,若是红球,则小李获胜;小李把摸出的球放回盒子里摇匀,由小马随机摸出一个球,若为黄球,则小马获胜.
(1)当m=4时,求小李摸到红球的概率是多少?
(2)当m为何值时,游戏对双方是公平的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com