Question

【题目】如图1，在△ABC中，AC＝BC，∠ACB＝90°，CE与AB相交于点D，且BE⊥CE，AF⊥CE，垂足分别为点E、F．

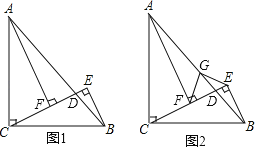
（1）若AF＝5，BE＝2，求EF的长．

（2）如图2，取AB中点G，连接FC、EC，请判断△GEF的形状，并说明理由．

Answer 1

【答案】（1）EF＝3；（2）△GEF为等腰直角三角形；理由见解析.

【解析】

（1）证得∠ACF＝∠CBE，由AAS证得△ACF≌△CBE得出CF＝BE＝2，AF＝CE＝5，即可得出结果；

（2）连接CG，证得CG⊥AB，∠BCG＝∠ACB＝45°，则∠CBG＝45°，推出∠GCB＝∠CBG＝45°，得出CG＝BG，易证∠FAD＝∠EBG，由△ACF≌△CBE得出CF＝BE，∠CAF＝∠BCE，证出∠FAD＝∠GCD，∠EBG＝∠FCG，由SAS证得△CFG≌△BEG得出FG＝EG，∠CGF＝∠EGB，由∠CGF+∠FGD＝90°，得出∠FGD+∠EGB＝90°，即∠FGE＝90°，即可得出结论．

（1）∵BE⊥CE，

∴∠BEC＝90°，

∵∠ACB＝90°，

∴∠BEC＝∠ACB，

∴∠ACF+∠BCE＝∠BCE+∠CBE＝90°，

∴∠ACF＝∠CBE，

∵AF⊥CE，

∴∠AFC＝90°，

在△ACF和△CBE中，

∵∠ACF=∠CBE，∠AFC=∠BEC，AC=BC，

∴△ACF≌△CBE（AAS），

∴CF＝BE＝2，AF＝CE＝5，

∵EF＝CE﹣CF，

∴EF＝5﹣2＝3；

（2）△GEF为等腰直角三角形；理由如下：

连接CG，如图2所示：

∵AC＝BC，AG＝BG，

∴CG⊥AB，∠BCG＝∠ACB＝×90°＝45°，

∴∠CBG＝90°﹣45°＝45°，

∴∠GCB＝∠CBG＝45°，

∴CG＝BG，

在△ADF和△BDE中，∵∠AFD＝∠BED，

∴∠FAD＝∠EBG，

由（1）证可知：△ACF≌△CBE，

∴CF＝BE，∠CAF＝∠BCE，

∵∠CAF+∠FAD＝∠GCD+∠BCE＝45°，

∴∠FAD＝∠GCD，

∴∠EBG＝∠FCG，

在△CFG与△BEG中，

∵CG=BG，∠FCG=∠EBG，CF=BE，

∴△CFG≌△BEG（SAS），

∴FG＝EG，∠CGF＝∠EGB，

∵∠CGF+∠FGD＝90°，

∴∠FGD+∠EGB＝90°，即∠FGE＝90°，

∴△FGE是等腰直角三角形．