
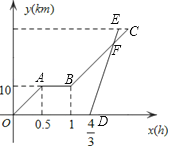
����Ŀ����ĩ��С�����һ�������г��Ӽ�����������Ϻ����棬�Ӽҳ���0.5Сʱ����Ϫ��������һ��ʱ���ԭ��ǰ�����Ϻ���С�����80���Ӻְּݳ�����ͬ·��ǰ�����Ϻ�����ͼ��������ҵ�·��y��km����С�����ʱ��x��h���ĺ���ͼ����֪�ְּݳ����ٶ���С���ﳵ�ٶȵ�3����
��1��С���ﳵ���ٶ�Ϊ_____km/h���ְּݳ����ٶ�Ϊ_____km/h.
��2��С���Ӽҵ���Ϫ����·��y��ʱ��x�ĺ�����ϵʽΪ_____��������Ϫ�������Ϻ���·��y��ʱ��x�ĺ�����ϵʽΪ______���ְִӼҵ����Ϻ���·�̣���ʱ��x�ĺ�����ϵʽΪ______.
��3��С���Ӽҳ�������Сʱ�ְ��ϣ���ʱ��Ҷ�Զ��
��4�����С���Ȱְ���10���ӵ�����Ϻ�����ô���Ϻ�����ж�Զ��

���𰸡���1��20��60����2��y��20x��y��20x��10��y��60x��80����3��С������1.75Сʱ��105���ӣ����ְ��ϣ���ʱ���25km����4�����Ϻ������30km��
��������
��1������ͼ��������С���ڼ������ʱ�䣬���ٶȣ�·����ʱ��Ϳ������С���ﳵ���ٶȣ���2��ֱ�����ô���ϵ�����Ϳ�������Ӽҵ���Ϫ���ʹ���Ϫ�������Ϻ�·��y��km����ʱ��x��h���ĺ�����ϵʽ����3������BC��DE����ʽ������Ԫһ�η����飬������������Ϳ���������ۣ���4����Ӱְ���С���ĵص㵽���Ϻ���·��Ϊn��km�������ݰְֱ�С���絽10�����г��й�n�ķ��̣����nֵ���ɣ�
��1����ͼ��ɵã�
С���ﳵ���ٶ�Ϊ��10��0.5��20km/h��
�ְּ߰ݳ����ٶ���С���ﳵ�ٶȵ�3����
��ְּݳ����ٶ�Ϊ��20��3��60km/h��
�ʴ�Ϊ��20��60��
��2����С���Ӽҵ���Ϫ����·��y��ʱ��x�ĺ�����ϵʽΪy��kx��
��0.5k��10��
���k��20��
��С���Ӽҵ���Ϫ����·��y��ʱ��x�ĺ�����ϵʽ��y��20x��
��С����OA������BC���ٶȲ��䣬
��OA��BC��
��ֱ��BC����ʽΪy��20x+b1��
�ѵ�B��1��10�������10=20+b1��
��ã�b1����10��
��y��20x��10��
���ٶ�=![]() =k��
=k��
��DE����ʽ��k=60��
��ֱ��DE����ʽΪy��60x+b2���ѵ�D��![]() ��0������ã�60��
��0������ã�60��![]() +b2=0��
+b2=0��
��ã�b2����80��
��y��60x��80.
�ʴ�Ϊ��y��20x��y��20x��10��y��60x��80��
��3����������ɵã�![]() ��
��
���![]() ��
��
��С������1.75Сʱ��105���ӣ����ְ��ϣ���ʱ���25km.
��4����Ӱְ���С���ĵص㵽���Ϻ���·��Ϊn��km����
��С���Ȱְ���10���ӵ�����Ϻ���
��![]() ��
��
��ã�n��5
��Ӽҵ����Ϻ���·��Ϊ5+25��30��km����
�𣺲��Ϻ������30km��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ��һ�����Ϊ150ƽ���ij�������������Ϊ�˽�Լ���ϣ�����һ�߿���ԭ�е�һ��ǽ��ǽ��Ϊ18�ף������������Χ�ɣ�����ʳ���Ϊ35�ף���Ҫ�����ꡣ���ij�������Ƕ����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() .
.
��1����ͼ1����֤��![]() ��
��
��2����ͼ2����![]() ƽ��
ƽ��![]() ����֤��
����֤��![]() ��
��
��3����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ������������
������������![]() ______.
______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���³�����ڴ���װ�ˡ�����ʽ���ˡ�����ͼ1��ʾ����A������ת����֧�㣬��E���������ε�����㣮����������ʱ������AEF���ֻ��������ͼ2��ʾ��λ�ã���ʾ��ͼ��ͼ3��ʾ�����˿��Ⱥ��Բ��ƣ�������AB��BC��EF��BC����AEF=143����AB=AE=1.2�ף���ô�ʺϸõ��³���ij����߱�־��Ϊ�� �����ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��

A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У�������ͼ��ʾ��ƽ��ֱ������ϵxOy����ABC���������㶼�ڸ���ϣ���A�����꣨4��4���������������⣺
��1��������ABC����y��ԳƵġ�A1B1C1����д����A1��B1��C1�����ꣻ
��2������ABC�Ƶ�C��ʱ����ת90����������ת��ġ�A2B2C2���������A��A2��·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������ABC�ı߳�Ϊ4��AD��BC���ϵ�������F��AD���ϵĶ�����E��AC����һ������AE��2����EF��CFȡ����Сֵʱ����ECF�Ķ���Ϊ( )

A. 20�� B. 25�� C. 30�� D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC��С��ͬѧ����ֱ�ߺ�Բ����������²�����

������BAC��ƽ����AM��BC�ڵ�D��
������AB�Ĵ�ֱƽ����EF��EF��AM�ཻ�ڵ�P��
������PB��PC��
����۲�ͼ�ν���������⣺
��1���߶�PA��PB��PC֮���������ϵ���� ����
��2������ABC��70�㣬���BPC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
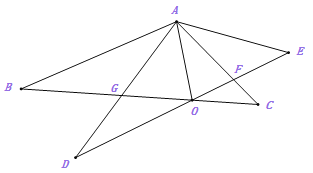
����Ŀ����ͼ,AM����ABC������,D���߶�AM��һ��(�����A�غ�)DE��AB��AC�ڵ�F,CE��AM,����AE.
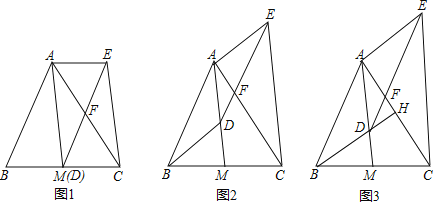
(1)��ͼ1,����D��M�غ�ʱ,��֤:�ı���ABDE��ƽ���ı���;
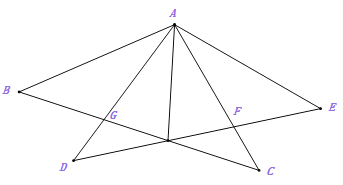
(2)��ͼ2,����D����M�غ�ʱ,(1)�еĽ��ۻ�������?��˵������.
(3)��ͼ3,�ӳ�BD��AC�ڵ�H,��BH��AC,��BH=AM
�����CAM�Ķ���;
�ڵ�FH=![]() , DM=4ʱ,��DH�ij�.
, DM=4ʱ,��DH�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����BAC=120����AE=BE��DΪEC�е㣮

��1������CAE�Ķ�����
��2����֤����ADE�ǵȱ������Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com