
【题目】如图,△ABC中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:

①作∠BAC的平分线AM交BC于点D;
②作边AB的垂直平分线EF,EF与AM相交于点P;
③连接PB,PC.
请你观察图形解答下列问题:
(1)线段PA,PB,PC之间的数量关系是 ;
(2)若∠ABC=70°,求∠BPC的度数.
【答案】(1)PA=PB=PC;(2)∠BPC=80°.
【解析】
(1)根据线段的垂直平分线的性质可得:PA=PB=PC;
(2)根据等腰三角形的性质得:∠ABC=∠ACB=70°,由三角形的内角和得:∠BAC=40°,由角平分线定义得:∠BAD=∠CAD=20°,最后利用三角形外角的性质可得结论.
(1)PA=PB=PC.理由如下:
∵AB=AC,AM平分∠BAC,∴AD是BC的垂直平分线,∴PB=PC.
∵EP是AB的垂直平分线,∴PA=PB,∴PA=PB=PC.
故答案为:PA=PB=PC;
(2)∵AB=AC,∴∠ABC=∠ACB=70°,∴∠BAC=180°﹣2×70°=40°.
∵AM平分∠BAC,∴∠BAD=∠CAD=20°.
∵PA=PB=PC,∴∠ABP=∠BAP=∠ACP=∠CAP=20°,∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个内角的平分线交于点O,延长BA到点D,使AD=AO,连接DO,若BD=BC,∠ABC=54![]() ,则∠BCA的度数为________.
,则∠BCA的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ADE中,∠DAE=90°,C是边AE上任意一点(点C与点A、E不重合),以AC为一直角边在Rt△ADE的外部作Rt△ABC,∠BAC=90°,连接BE、CD.
(1)在图1中,若AC=AB,AE=AD,现将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图2,那么线段BE.CD之间有怎样的关系,写出结论,并说明理由;
(2)在图1中,若CA=3,AB=5,AE=10,AD=6,将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图3,连接BD、CE.
①求证:△ABE∽△ACD;
②计算:BD2+CE2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和哥哥一起骑自行车从家里出发到昌南湖游玩,从家出发0.5小时后到达陶溪川,游玩一段时间后按原速前往昌南湖.小明离家80分钟后,爸爸驾车沿相同路线前往昌南湖,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知爸爸驾车的速度是小明骑车速度的3倍.
(1)小明骑车的速度为_____km/h,爸爸驾车的速度为_____km/h.
(2)小明从家到陶溪川的路程y与时间x的函数关系式为_____,他从陶溪川到昌南湖的路程y与时间x的函数关系式为______,爸爸从家到昌南湖的路程,与时间x的函数关系式为______.
(3)小明从家出发多少小时后被爸爸追上?此时离家多远?
(4)如果小明比爸爸晚10分钟到达昌南湖,那么昌南湖离家有多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
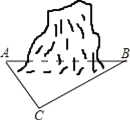
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,下列结论正确的是( )
①BD=CE②△BDF,△CEF都是等腰三角形③BD+CE=DE④△ADE的周长为AB+AC.
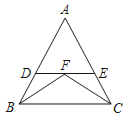
A.①②B.③④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:综合实践活动课上,同学们围绕“已知三角形三边的长度,求三角形的面积”开展活动,启航小组同学想到借助正方形网格解决问题
问题解决:图(1)、图(2)都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,操作发现,启航小组同学在图(1)中画出△ABC,其顶点A,B,C都在格点上,同时构造长方形CDEF,使它的顶点都在格点上,且它的边EF经过点A,ED经过点B.同学们借助此图求出了△ABC的面积.
(1)在图(1)中,△ABC的三边长分别是AB= ,BC= ,AC= .△ABC的面积是 .
(2)已知△PMN中,PM=![]() ,MN=2
,MN=2![]() ,NP=
,NP=![]() .请你根据启航小组的思路,在图(2)中画出△PMN,并直接写出△RMN的面积 .
.请你根据启航小组的思路,在图(2)中画出△PMN,并直接写出△RMN的面积 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B,C重合)将线段AD绕点A逆时针旋转90°得到AE,连接EC.求证:△ABD≌△ACE;
(2)探索:如图2,在Rt△ABC与Rt△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段BD2、CD2、DE2之间满足的等量关系,并证明你的结论;
(3)应用:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=6,CD=2,求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com