
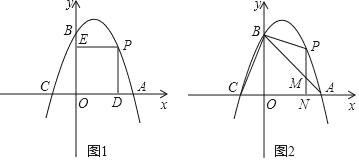
����Ŀ����ͼ1��������y����x2+bx+c������A��2��0����B��0��2������x�ύ����һ��C��
��1���������ߵĽ���ʽ����C�����ꣻ
��2����P��������y����x2+bx+c�ڵ�һ�����ϵĵ㣬����P�ֱ���x�ᡢy�������ߣ�����ֱ�ΪD��E�����ı���ODPE���ܳ������ֵ��
��3����ͼ2����P��������y����x2+bx+c�ڵ�һ�����ϵĵ㣬����P��PN��x�ᣬ����ΪN����AB��M������PB��PA�����P�ĺ�����Ϊt������ABP��������ڡ�ABC�����![]() ʱ����t��ֵ��
ʱ����t��ֵ��
���𰸡���1������1��0������2���ı���ODPE�ܳ����ֵΪ6����3����t��1ʱ����ABP��������ڡ�ABC�������![]() ��
��
��������
��1������A�͵�B��������������ߵĽ���ʽ�����b��c��ֵ���Ӷ��õ������ߵĽ���ʽ��Ȼ����y��0�ɵõ�����x�ķ��̣��ⷽ�̼�����õ�C�����ꣻ��2�����P������Ϊ��t����t2+t+2�����ú�t��ʽ�ӱ�ʾ��PE��PD�ij��ȣ�Ȼ��ɵõ��ı���ODPE���ܳ���t�ĺ�����ϵʽ����������䷽������õ�P�ĺ����꣬�Լ��ı���ODPE�ܳ������ֵ��������3�������ֱ��AB�Ľ���ʽ����P�������Ϊ��t����t2+t+2�������M������Ϊ��t����t+2�����������PM����t2+2t����S��ABP��S��PMB+S��PMA�ɵõ���ABP�������t�ĺ�����ϵʽ��Ȼ���ٸ��ݣ���ABP�����������ABC�������![]() �з�����⼴�ɣ�
�з�����⼴�ɣ�
�⣺��1������A�͵�B���������y����x2+bx+c�ã�![]() ��
��
��ã�b��1��c��2��
�������ߵĽ���ʽΪy����x2+x+2��
��y��0����0����x2+x+2����ã�x��2��x����1��
���C����������1��0����
��2�����P��������t����t2+t+2������PE��t��PD����t2+t+2��
���ı���ODPE���ܳ���2����t2+t+2+t������2��t��1��2+6��
�൱P������Ϊ��1��2��ʱ��
���ı���ODPE�ܳ����ֵΪ6��
��3����A��2��0����B��0��2����
��AB�Ľ���ʽΪy����x+2��
��P��ĺ�����Ϊt��
��P����������t2+t+2��
�֡�PN��x�ᣬ
��M���������t����t+2����
��PM����t2+t+2������t+2������t2+2t��
��S��ABP��S��PMB+S��PMA��![]() PMON+
PMON+![]() PMAN��
PMAN��![]() PMOA����t2+2t��
PMOA����t2+2t��
�֡�S��ABC��![]() ACOB��
ACOB��![]() ��3��2��3��
��3��2��3��
����t2+2t��3��![]() ����ã�t1��t2��1��
����ã�t1��t2��1��
�൱t��1ʱ����ABP�����������ABC�������![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ����ཻ�ڵ�O��DE��CA��AE��BD��
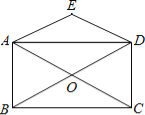
��1����֤���ı���AODE�����Σ�
��2�����������С�����ABCD����һ������Ϊ������ABCD���������������䣬���ı���AODE����״��ʲô��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
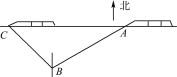
����Ŀ����ͼ���ھ�������200 m��B�����۲�Ӽؿ����ҵص�����г������������������ͷ��A��ʱ��ǡ��λ��B���ı�ƫ��60��������.10 s������ͷ����C����ǡ��λ��B�������������ϣ������ж�����ƽ��������________ m/s(�����������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0����ͼ����ͼ���������ĸ����ۣ���abc��0����b2��4ac��0����a+b+c��0����b��2a��������ȷ�ĸ����ǣ�������
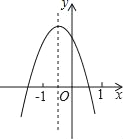
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
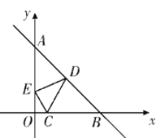
����Ŀ����ͼ��ʾ����֪��C(1��0)��ֱ��![]() ����������ֱ���A��B���㣬D��E�ֱ����߶�AB��OA�ϵĶ��㣬���CDE���ܳ�����Сֵ��( )
����������ֱ���A��B���㣬D��E�ֱ����߶�AB��OA�ϵĶ��㣬���CDE���ܳ�����Сֵ��( )
A.![]() B.10
B.10
C.![]() D.12
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
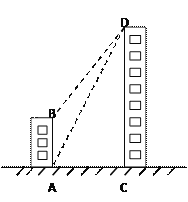
����Ŀ����ͼ��һ������¥AB�ĸ�Ϊ16�ף�Զ����һ������¥CD��С���ھ���¥��¥��A���������¥��D��������Ϊ![]() ����������¥��¥��D����þ���¥��¥��B���ĸ���Ϊ
����������¥��¥��D����þ���¥��¥��B���ĸ���Ϊ![]() ������A��C����ֱ�λ��B��D��������·�����A��C������ͬһˮƽ���ϣ�������¥CD�ĸ߶ȣ�
������A��C����ֱ�λ��B��D��������·�����A��C������ͬһˮƽ���ϣ�������¥CD�ĸ߶ȣ�
(�ο����ݣ� ![]() ��
�� ![]() .�����ȷ��0.1��)
.�����ȷ��0.1��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
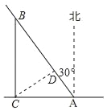
����Ŀ����ͼ��һ����ij��ǽC��������10���ﴦ��A�㣬��25����/ʱ���ٶ��ر�ƫ��30�㷽���У�
��1���ʶʱ�������������
��2�������������������ʱ�����˶��ٺ����ʱ����������ж�Զ��������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ������ѧ���п�չ��ɳ�����������������������������Ŀ�Ļ��Ϊ�˽�ѧ����������Ŀ��ϲ���������������˸�Уm��ѧ����ϲ����һ����Ŀ��ÿ��ѧ����ѡ��ֻ��ѡ�����ֻ��Ŀ��һ�֣����������������Ƴ����µIJ�������ͳ��ͼ����
ѧ����ϲ���Ļ��Ŀ������ͳ�Ʊ�
��Ŀ | ѧ���������� | �ٷֱ� |
��ɳ�� | 20 | 10% |
������ | 60 | p% |
������ | n | 40% |
����� | 40 | 20% |
����ͼ�����ṩ����Ϣ������������⣺
��1��m= ��n= ��p= ��
��2�������������Ϣֱ�Ӳ�ȫ����ͳ��ͼ��

��3�����ݳ�����������������Ƹ�У2000��ѧ�����ж�����ѧ����ϲ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
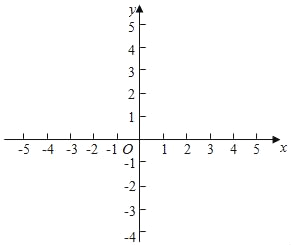
����Ŀ����ƽ��ֱ������ϵ�У�������y��ax2+bx+3������A��3��0���͵�B��4��3����
��1������������������Ӧ�Ķ��κ����ı���ʽ��
��2��ֱ��д���������߿��ڷ���Ͷ������꣮
��3��ֱ������������ƽ���ڻ������������ߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com