
【题目】如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
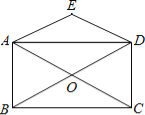
(1)求证:四边形AODE是菱形;
(2)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE的形状是什么?说明理由.
【答案】(1)证明见解析;(2)矩形,理由见解析.
【解析】
试题(1)根据矩形的性质求出OA=OD,证出四边形AODE是平行四边形即可;(2)根据菱形的性质求出∠AOD=90°,再证出四边形AODE是平行四边形即可.
试题解析:(1)∵矩形ABCD的对角线相交于点O,
∴AC=BD(矩形对角线相等),OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD(矩形对角线互相平分).∴OA=OD .
BD(矩形对角线互相平分).∴OA=OD .
∵DE∥CA ,AE∥BD,∴四边形AODE是平行四边形(两组对边分别平行的四边形是平行四边形).
∴四边形AODE是菱形(一组邻边相等的平行四边形是菱形).
(2)矩形,理由如下:
∵DE∥CA,AE∥BD,∴四边形AODE是平行四边形.
∵菱形ABCD,∴AC⊥BD. ∴∠AOD=90°.
∴平行四边形AODE是矩形.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G,E,D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
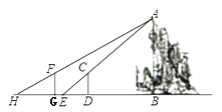
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
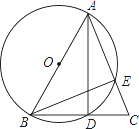
(1)求证:D是BC的中点;
(2)求证:△BEC∽△ADC;
(3)若CE=5,BD=6.5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:

①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( )

A. 4﹣2π B. 8+π C. 4﹣π D. 8﹣2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c的图象中,王刚同学观察得出了下面四条信息:(1)b2﹣4ac>0;(2)c>1;(3)2a﹣b<0;(4)a+b+c<0,其中错误的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周长;
, AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
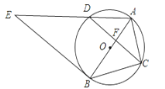
查看答案和解析>>
科目:初中数学 来源: 题型:
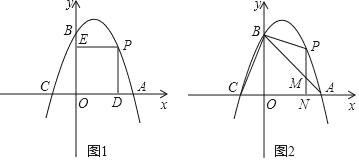
【题目】如图1,抛物线y=﹣x2+bx+c经过点A(2,0),B(0,2),与x轴交于另一点C.
(1)求抛物线的解析式及点C的坐标;
(2)点P是抛物线y=﹣x2+bx+c在第一象限上的点,过点P分别向x轴、y轴作垂线,垂足分别为D,E,求四边形ODPE的周长的最大值;
(3)如图2,点P是抛物线y=﹣x2+bx+c在第一象限上的点,过点P作PN⊥x轴,垂足为N,交AB于M,连接PB,PA.设点P的横坐标为t,当△ABP的面积等于△ABC面积的![]() 时,求t的值.
时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com