【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．
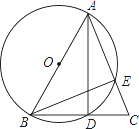
（1）求证：D是BC的中点；
（2）求证：△BEC∽△ADC；
（3）若CE=5,BD=6.5,求AB的长.
【答案】（1）证明见解析; （2）证明见解析; （3）10．
【解析】
试题（1）根据圆周角定理的推论得到∠BDA=90°，再根据等腰三角形的性质即可得到BD=CD；
（2）根据有两对角相等的两个三角形相似证明即可；
（3）由（2）中的三角形相似可得到关于AC的比例式，AC可求，进而求出AB的长．
试题解析：（1）∵AB为⊙O的直径，∴∠BDA=90°.∴AD⊥BC．
∵AB=AC．∴BD=CD.∴D是BC的中点.
（2）∵AB=AC，∴∠C=∠ABD.
∵AB为⊙O的直径，∴∠ADB=∠BEC=90°.
∴△BEC∽△ADC.
（3）∵△BEC∽△ADC，∴CE：BD=BC：AC.
∵CE=5，BD=6.5，∴BC=2BD=13.
∴5：6.5=13：AC，∴AC=10.
∴AB=AC=10．
科目：初中数学 来源： 题型：
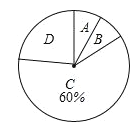
【题目】今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．
评估成绩n（分） | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n＜90 | B | |
70≤n＜80 | C | 15 |
n＜70 | D | 6 |
根据以上信息解答下列问题：
（1）求m的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）
（3）从评估成绩不少于80分的连锁店中任选2家介绍营销经验，求其中至少有一家是A等级的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△OAB中，OA=4，AB=5，点C在OA上，AC=1，⊙P的圆心P在线段BC上，且⊙P与边AB，AO都相切．若反比例函数
（k≠0）的图象经过圆心P，则k=________________。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+c（a，b，c为常数，且a≠0）经过点（﹣1，0）和（m，0），且1＜m＜2，当x＜﹣1时，y随着x的增大而减小．下列结论：
①abc＞0；
②a+b＞0；
③若点A（﹣3，y1），点B（3，y2）都在抛物线上，则y1＜y2；
④a（m﹣1）+b=0；
⑤若c≤﹣1，则b2﹣4ac≤4a．
其中结论错误的是 ．（只填写序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
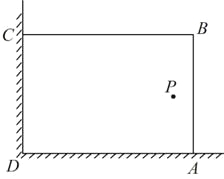
【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm.
（1）若花园的面积为192m2, 求x的值；
（2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD的对角线相交于点O，DE∥CA，AE∥BD．
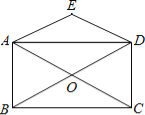
（1）求证：四边形AODE是菱形；
（2）若将题设中“矩形ABCD”这一条件改为“菱形ABCD”，其余条件不变，则四边形AODE的形状是什么？说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝x2－2x－3的图象与x轴交于A、B两点（A在B的左侧）,与y轴交于点C,顶点为D．
（1）求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
（2）说出抛物线y＝x2－2x－3可由抛物线y＝x2如何平移得到？
（3）求四边形OCDB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图，则下列四个结论：①abc＞0；②b2﹣4ac＞0；③a+b+c＜0；④b＞2a．其中正确的个数是（ ）
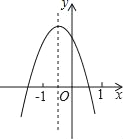
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
