
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。

【答案】![]()
【解析】分析:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,用面积法可求出⊙P的半径,然后通过三角形相似可求出CD,从而得到点P的坐标,就可求出k的值.
详解:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,如图所示.
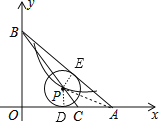
则有PD⊥OA,PE⊥AB.
设⊙P的半径为r,
∵AB=5,AC=1,
∴S△APB= ![]() ABPE=
ABPE=![]() r,S△APC=
r,S△APC=![]() ACPD=
ACPD=![]() r.
r.
∵∠AOB=90°,OA=4,AB=5,
∴OB=3.
∴S△ABC=![]() ACOB=
ACOB=![]() ×1×3=
×1×3=![]() .
.
∵S△ABC=S△APB+S△APC,
∴![]() =
=![]() r+
r+![]() r.
r.
∴r=![]() .
.
∴PD=![]() .
.
∵PD⊥OA,∠AOB=90°,
∴∠PDC=∠BOC=90°.
∴PD∥BO.
∴△PDC∽△BOC.
∴![]() .
.
∴PDOC=CDBO.
∴![]() ×(4-1)=3CD.
×(4-1)=3CD.
∴CD=![]() .
.
∴OD=OC-CD=3-![]() =
=![]() .
.
∴点P的坐标为(![]() ,
,![]() ).
).
∵反比例函数y=![]() (k≠0)的图象经过圆心P,
(k≠0)的图象经过圆心P,
∴k=![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
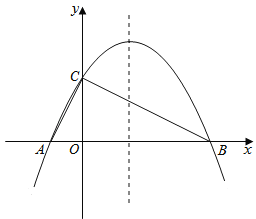
【题目】如图,已知抛物线y=﹣![]() x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式及它的对称轴;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
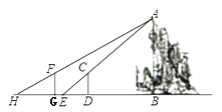
【题目】假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G,E,D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
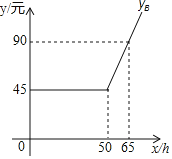
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的一个二次函数,其图象沿x轴翻折后,得到的图象所对应的二次函数称为原二次函数的横翻函数.
(1)直接写出二次函数y=2x2的横翻函数的表达式.
(2)已知二次函数y=x2+bx+c的图象经过点A(﹣3,1)、B(2,6).
①求b、c的值.
②求二次函数y=x2+bx+c的横翻函数的顶点坐标.
③若将二次函数y=x2+bx+c的图象位于A、B两点间的部分(含A、B两点)记为G,则当二次函数y=﹣x2﹣bx﹣c+m与G有且只有一个交点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
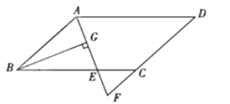
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=![]() ,则△EFC的面积是( )
,则△EFC的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
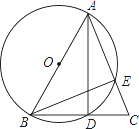
(1)求证:D是BC的中点;
(2)求证:△BEC∽△ADC;
(3)若CE=5,BD=6.5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
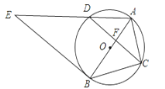
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周长;
, AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com