
����Ŀ�����壺���ڸ�����һ�����κ�������ͼ����x�ᷭ�ۺõ���ͼ������Ӧ�Ķ��κ�����Ϊԭ���κ����ĺᷭ������
��1��ֱ��д�����κ���y��2x2�ĺᷭ�����ı���ʽ��
��2����֪���κ���y��x2+bx+c��ͼ����A����3��1����B��2��6����
����b��c��ֵ��
������κ���y��x2+bx+c�ĺᷭ�����Ķ������꣮
���������κ���y��x2+bx+c��ͼ��λ��A��B�����IJ��֣���A��B���㣩��ΪG�����κ���y����x2��bx��c+m��G����ֻ��һ������ʱ��ֱ��д��m��ȡֵ��Χ��
���𰸡���1��y����2![]() ��2����b=2,c=-2 �ڣ���1��3�� ��m����6��2��m��12
��2����b=2,c=-2 �ڣ���1��3�� ��m����6��2��m��12
��������
��1�����ݺᷭ�����Ķ�����.
(2)������֪�㣬�����a,b���ɵú�������ʽ.������ᷭ�����ı���ʽ����֮����������.��A��B���뺯�����ٸ������⼴����m�ķ�Χ.
�⣺��1���ɺᷭ�����Ķ���֪�����κ���y��2x2�ĺᷭ�����ı���ʽ��y����2x2��
��2���١߶��κ���y��x2+bx+c��ͼ����A����3��1����B��2��6����
��![]()
���![]()
��b��ֵΪ2��c��ֵΪ��2��
�ڡ߶��κ���y��x2+bx+c�ı���ʽΪy��x2+2x��2��
�����ĺᷭ�����ı���ʽΪy����x2��2x+2
��y����x2��2x+2������x+1��2+3��
����κ���y��x2+bx+c�ĺᷭ�����Ķ�������Ϊ����1��3����
�۵�A����3��1��������κ���y����x2��2x+2+m���é�9+6+2+m��1�����m��2��
��B��2��6��������κ���y����x2��2x+2+m���é�4��4+2+m��6�����m��12��
�������غ�ʱ��m����6��
��m���������Ϊm����6��2��m��12��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A����1��0����B��2����3��������һ�κ���y1����x+m����κ���y2��ax2+bx��3��ͼ���ϣ�
��1����m��ֵ�Ͷ��κ����Ľ���ʽ��
��2����ֱ��д��ʹy1��y2ʱ�Ա���x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
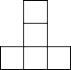
����Ŀ�������ɸ�С��������һ�������壬ʹ�������濴������濴������ͼ��ͬһ��ͼ��ͨ��ʵ�ʲ���������ͬѧ�����ۣ�����������⣺
��1������Ҫ��С������ĸ����Ƕ��٣������ҳ����֣�
��2����������������ٺ�����������ļ���������濴����ͼ������С��������ע���ڸ�λ����С������ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ���ӵĺ��������ͼ��ʾ���ı���BACD������AB��CD���t��̨PC��ǰ��ˮ�����������洬M��N���۲�Ա�ڲt��̨����P���۲��洬M�ĸ���![]() ���۲��洬N�ڸ���
���۲��洬N�ڸ���![]() ����֪NM����ֱ����PC����ֱ�ߴ�ֱ������Ϊ��E��PE��Ϊ30�ף�
����֪NM����ֱ����PC����ֱ�ߴ�ֱ������Ϊ��E��PE��Ϊ30�ף�
��1�������洬M��N֮��ľ��루�����ȷ��1�ף���
��2����֪�Ӹ�24�ף��ӳ�100�ף���ˮ��AD���¶�![]() ��Ϊ��ߴ�ӷ���������ijʩ�����ڴ�ӵı�ˮ��������ʯ���ӹ̣��ӹ̺�Ӷ��ӿ�3�ף���ˮ��FH���¶�Ϊ
��Ϊ��ߴ�ӷ���������ijʩ�����ڴ�ӵı�ˮ��������ʯ���ӹ̣��ӹ̺�Ӷ��ӿ�3�ף���ˮ��FH���¶�Ϊ![]() ��ʩ��12���Ϊ������ɼӹ�����ʩ���������˻�е�豸������Ч����ߵ�ԭ����1��5���������ԭ�ƻ���ǰ20����ɼӹ�����ʩ����ԭ�ƻ�ƽ��ÿ��������ʯ�����������ף����ο����ݣ�
��ʩ��12���Ϊ������ɼӹ�����ʩ���������˻�е�豸������Ч����ߵ�ԭ����1��5���������ԭ�ƻ���ǰ20����ɼӹ�����ʩ����ԭ�ƻ�ƽ��ÿ��������ʯ�����������ף����ο����ݣ� ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ִ���λ�ڵ���P�ı�ƫ��30�㷽�������120�����A�����ִ������Ϸ�����һ��ʱ�����λ�ڵ���P����ƫ��64�㷽���ϵ�B�������ִ����ڵ�B�������P�ľ��룮�������ȷ��0.1������ο����ݣ�sin64�㣽0.90��cos64�㣽0.44��tan64�㣽2.05��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��OAB�У�OA=4��AB=5����C��OA�ϣ�AC=1����P��Բ��P���߶�BC�ϣ��ҡ�P���AB��AO�����У�������������![]() ��k��0����ͼ��Բ��P����k=________________��
��k��0����ͼ��Բ��P����k=________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������Σ����ǵ��ܳ��ֱ���36��12���ܳ��ϴ�������ε�����Ϊ15���ܳ���С�������ε���С��Ϊ3�����ܳ��ϴ�������ε�����ǣ�������
A. 52 B. 54 C. 56 D. 58
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
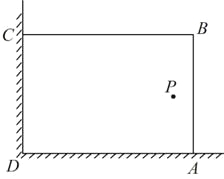
����Ŀ��������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ�ǣ������㹻��������28m�������Χ��һ�����λ�ABCD�����ֻΧAB��BC���ߣ�����AB=xm.
��1�����������Ϊ192m2, ��x��ֵ��
��2������P����һ������ǽCD��AD�ľ���ֱ���15m��6m��Ҫ�������Χ�ڻ��ڣ����߽磬���������Ĵ�ϸ���������S�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��A ��-1,0)��B ��5,0)���㣬ֱ��
�ύ��A ��-1,0)��B ��5,0)���㣬ֱ��![]() ��y�ύ�ڵ�
��y�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��x���Ϸ�����������һ���㣬����
��x���Ϸ�����������һ���㣬����![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��
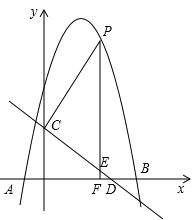
��1���������ߵĽ���ʽ��
��2����![]() ����
����![]() ��ֵ��
��ֵ��
��3������![]() �ǵ�
�ǵ�![]() ����ֱ��
����ֱ��![]() �ĶԳƵ㣬�Ƿ���ڵ�
�ĶԳƵ㣬�Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ����
����![]() ���ϣ������ڣ���ֱ��д����Ӧ�ĵ�
���ϣ������ڣ���ֱ��д����Ӧ�ĵ�![]() �����ꣻ�������ڣ���˵��������
�����ꣻ�������ڣ���˵��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com