
【题目】某水库大坝的横截面是如图所示的四边形BACD,期中AB∥CD.瞭望台PC正前方水面上有两艘渔船M、N,观察员在瞭望台顶端P处观测渔船M的俯角![]() ,观测渔船N在俯角
,观测渔船N在俯角![]() ,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度![]() .为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为
.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为![]() ,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据:
,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据: ![]() )
)

【答案】20m;600立方米.
【解析】试题(1)根据已知求出EN,根据正切的概念求出EM,求差得到答案;
(2)根据坡度和锐角三角函数的概念求出截面积和土石方数,根据题意列出分式方程,解方程得到答案.
试题解析:(1)在Rt△PEN中,∵∠PNE=45°,
∴EN=PE=30米,
在Rt△PEM中,∠PME=31°,tan∠PME=![]() ,
,
∴ME=![]() ≈50(米),
≈50(米),
∴MN=EM-EN=20米,
答:两渔船M,N之间的距离约为20米;
(2)过点F作FK∥AD交AH于点K,过点F作FL⊥AH交直线AH于点L,
则四边形DFKA为平行四边形,

∴∠FKA=∠DAB,DF=AK=3,
由题意得,tan∠FKA=tan∠DAB=4,tan∠H=![]() ,
,
在Rt△FLH中,LH=![]() =36,
=36,
在Rt△FLK中,KL=![]() =6,
=6,
∴HK=30,AH=33,
梯形DAHF的面积为: ![]() ×DL×(DF+AH)=432,
×DL×(DF+AH)=432,
所以需填土石方为432×100=43200,
设原计划平均每天填x立方米,由题意得,
12x+(![]() -12-20)×1.5x=43200,
-12-20)×1.5x=43200,
解得,x=600,
经检验x=600是方程的解.
答:原计划平均每天填筑土石方600立方米.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】材料一:把一个自然数的个位数字截去,再用余下的数减去个位数的2倍,如果差是7的倍数,则原数能被7整除.如果差太大不易看出是否7的倍数,可重复上述「截尾、倍大、相减、验差」的过程,直到能清楚判断为止.例如,判断392是否7的倍数的过程如下:![]() ,
,![]() ,所以,392是7的倍数;又例如判断8638是否7的倍数的过程如下:
,所以,392是7的倍数;又例如判断8638是否7的倍数的过程如下:![]() ,
,![]() ,
,![]() ,所以,8638是7的倍数.
,所以,8638是7的倍数.
材料二:若一个四位自然数n满足千位与个位相同,百位与十位相同,我们称这个数为“对称数”.将“对称数”n的前两位与后两位交换位置得到一个新的“对称数”![]() ,记
,记![]() ,例如
,例如![]() .
.
(1)请用材料一的方法判断6909与367能不能被7整除;
(2)若m、p是“对称数”,其中![]() ,
,![]() (
(![]() ,
,![]() 且a,b,c均为整数),若m能被7整除,且
且a,b,c均为整数),若m能被7整除,且![]() ,求p.
,求p.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G,E,D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
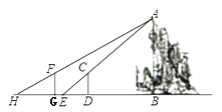
查看答案和解析>>
科目:初中数学 来源: 题型:
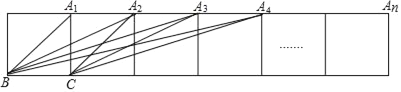
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
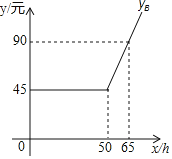
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的一个二次函数,其图象沿x轴翻折后,得到的图象所对应的二次函数称为原二次函数的横翻函数.
(1)直接写出二次函数y=2x2的横翻函数的表达式.
(2)已知二次函数y=x2+bx+c的图象经过点A(﹣3,1)、B(2,6).
①求b、c的值.
②求二次函数y=x2+bx+c的横翻函数的顶点坐标.
③若将二次函数y=x2+bx+c的图象位于A、B两点间的部分(含A、B两点)记为G,则当二次函数y=﹣x2﹣bx﹣c+m与G有且只有一个交点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c的图象中,王刚同学观察得出了下面四条信息:(1)b2﹣4ac>0;(2)c>1;(3)2a﹣b<0;(4)a+b+c<0,其中错误的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com