
【题目】抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3,y1),点B(3,y2)都在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤若c≤﹣1,则b2﹣4ac≤4a.
其中结论错误的是 .(只填写序号)
【答案】③⑤
【解析】
试题分析:根据题意画出抛物线的大致图象,利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,于是可对①进行判断;由于抛物线过点(﹣1,0)和(m,0),且1<m<2,根据抛物线的对称性和对称轴方程得到0<﹣![]() <
<![]() ,变形可得a+b>0,则可对②进行判断;利用点A(﹣3,y1)和点B(3,y2)到对称轴的距离的大小可对③进行判断;根据抛物线上点的坐标特征得a﹣b+c=0,am2+bm+c=0,两式相减得am2﹣a+bm+b=0,然后把等式左边分解后即可得到a(m﹣1)+b=0,则可对④进行判断;根据顶点的纵坐标公式和抛物线对称轴的位置得到
,变形可得a+b>0,则可对②进行判断;利用点A(﹣3,y1)和点B(3,y2)到对称轴的距离的大小可对③进行判断;根据抛物线上点的坐标特征得a﹣b+c=0,am2+bm+c=0,两式相减得am2﹣a+bm+b=0,然后把等式左边分解后即可得到a(m﹣1)+b=0,则可对④进行判断;根据顶点的纵坐标公式和抛物线对称轴的位置得到![]() <c≤﹣1,变形得到b2﹣4ac>4a,则可对⑤进行判断.
<c≤﹣1,变形得到b2﹣4ac>4a,则可对⑤进行判断.
解:如图,
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①的结论正确;
∵抛物线过点(﹣1,0)和(m,0),且1<m<2,
∴0<﹣![]() <
<![]() ,
,
∴![]() +
+![]() =
=![]() >0,∴a+b>0,所以②的结论正确;
>0,∴a+b>0,所以②的结论正确;
∵点A(﹣3,y1)到对称轴的距离比点B(3,y2)到对称轴的距离远,
∴y1>y2,所以③的结论错误;
∵抛物线过点(﹣1,0),(m,0),
∴a﹣b+c=0,am2+bm+c=0,
∴am2﹣a+bm+b=0,
a(m+1)(m﹣1)+b(m+1)=0,
∴a(m﹣1)+b=0,所以④的结论正确;
∵![]() <c,
<c,
而c≤﹣1,
∴![]() <﹣1,
<﹣1,
∴b2﹣4ac>4a,所以⑤的结论错误.
故答案为③⑤.
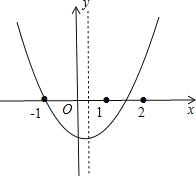


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图是一种躺椅及其简化结构示意图,扶手AB与座板CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,量得∠EOF=90°,∠ODC=30°,ON=40cm,EG=30cm.
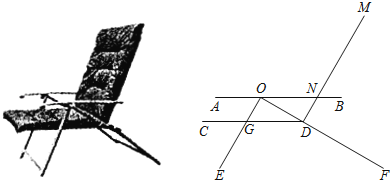
(1)求两支架落点E、F之间的距离;
(2)若MN=60cm,求躺椅的高度(点M到地面的距离,结果取整数).
(参考数据:sin60°=![]() ,cos60°=
,cos60°=![]() ,tan60°=
,tan60°=![]() ≈1.73,可使用科学计算器)
≈1.73,可使用科学计算器)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形属于因式分解的是( )
A. x2+5x-1=x(x+5)-1 B. x2-9=(x+3)(x-3)
C. x2-4+3x=(x+2)(x-2)+3x D. (x+2)(x-2)=x2-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个饲养场,鸡的只数与兔的只数之和是70,鸡、兔的腿数之和为196,若设鸡的只数是x,依题意可列方程为
A. 2x=196+4(70-x) B. 4x+2(70-x)=196
C. 2x+4(70-x)=196 D. 2x+196=4(70-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
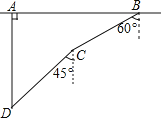
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com