
����Ŀ����ͼ��һ�����μ���ṹʾ��ͼ������AB������CD��ƽ���ڵ��棬����DM��֧��OEƽ�У�ǰ֧��OE���֧��OF�ֱ���CD���ڵ�G�͵�D��AB��DM���ڵ�N��������EOF=90������ODC=30����ON=40cm��EG=30cm��
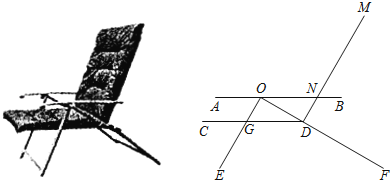
��1������֧�����E��F֮��ľ��룻
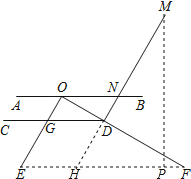
��2����MN=60cm�������εĸ߶ȣ���M������ľ��룬���ȡ��������
���ο����ݣ�sin60��=![]() ��cos60��=
��cos60��=![]() ��tan60��=
��tan60��=![]() ��1.73����ʹ�ÿ�ѧ��������
��1.73����ʹ�ÿ�ѧ��������
���𰸡���1��EF=100cm����2��95cm��
��������
�����������1������ƽ���߷��߶γɱ��������ó�![]() ������ƽ���ı��ε��ж������ʽ���������ɣ�
������ƽ���ı��ε��ж������ʽ���������ɣ�
��2�������ı���ONHE��ƽ���ı��Σ������ó�NH=OE=50cm����MHF=��E=60��������MP=110sin60��������ɣ�
�⣺��1������EF��
��CDƽ���ڵ��棬
��GD��EF��
��![]() ��
��
����AB��EF��
��AB��CD��
��OE��DM��
���ı���OGDN��ƽ���ı��Σ�
��OG=DN��GD=ON��
��ON=40cm����EOF=90������ODC=30�㣬
��GD=40cm��OG=![]() GD=20cm����EG=30cm��
GD=20cm����EG=30cm��
��![]() ����EF=100cm��
����EF=100cm��
��2���ӳ�MD��EF�ڵ�H������M��MP��EF�ڵ�P��
���ı���ONHE��ƽ���ı��Σ�
��NH=OE=50cm����MHF=��E=60����
����MN=60cm����MH=110cm��
��Rt��MHP��MP=MHsin��MHP��
��MP=110sin60��=110��![]() =55
=55![]() ��95��cm����
��95��cm����
�����εĸ߶�ԼΪ95cm��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����з������Ƕ�Ԫһ�η��̵��ǣ�������
A. 3x+y=0 B. 2x��1=4 C. 2x2��y=2 D. 2x+y=3z
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ�·ݵ�Ӫҵ��Ϊ36��Ԫ�����·ݵ�Ӫҵ��Ϊ48��Ԫ����ÿ�µ�ƽ��������Ϊx������з���Ϊ��������
A. 48��1��x��2=36 B. 48��1+x��2=36 C. 36��1��x��2=48 D. 36��1+x��2=48
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2��8x��1��0�䷽��ɱ���Ϊ(����)
A. (x��4)2��17 B. (x��4)2��15 C. (x��4)2��17 D. (x��4)2��15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ�������
A. a8��a2=a4 B. (��m)2(��m3)=��m5 C. x3+x3=x6 D. (a3)3=a6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε��ܳ�Ϊ15cm������һ�߳�Ϊ3cm����õ��������ε�����Ϊ ���� ��
A. 3cm B. 6cm C. 3cm��6cm D. 3cm��9cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��½�һ����Ʒ��ÿ���ɱ���25Ԫ������һ��ʱ�䷢��������y�����������۵���x��Ԫ/����֮���һ�κ�����ϵ�����±���
x��Ԫ/���� | 30 | 50 |
y������ | 190 | 150 |
��1����y��x֮��ĺ�����ϵʽ��
��2��������Ʒ�����۵�����45Ԫ��80Ԫ֮�両����
�����۵��۶�Ϊ����Ԫʱ�������������ʱ������Ϊ���٣�
���̳���Ҫ�����ʱ���ڻ��4 550Ԫ�������������۵���Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A��ʻ�����120 km��B�أ�����ƽ���ٶ���30 km/h����������B�ص�·��s(km)����ʻʱ��t(h)�ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��(����)
A. s��120��30t(0��t��4) B. s��120��30t(t��0)
C. s��30t(0��t��4) D. s��30t(t��4)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��a��b��cΪ��������a��0�������㣨��1��0���ͣ�m��0������1��m��2����x����1ʱ��y����x���������С�����н��ۣ�
��abc��0��
��a+b��0��
������A����3��y1������B��3��y2�������������ϣ���y1��y2��
��a��m��1��+b=0��
����c�ܩ�1����b2��4ac��4a��
���н��۴������ ����ֻ��д��ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com