
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.
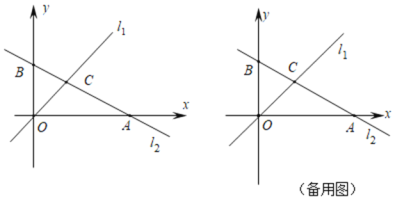
(1)求点![]() 的坐标;
的坐标;
(2)若直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,请求出点
,请求出点![]() 的坐标;
的坐标;
(3)在![]() 轴右侧、点
轴右侧、点![]() 左侧有一条平行于
左侧有一条平行于![]() 轴的动直线,分别与
轴的动直线,分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰直角三角形?若存在,请求出满足条件的所有点
为等腰直角三角形?若存在,请求出满足条件的所有点![]() 的坐标;若不存在;请说明理由.
的坐标;若不存在;请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在.满足条件的所有点
;(3)存在.满足条件的所有点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() .
.
【解析】
(1)联立![]() 与
与![]() ,即可求解;
,即可求解;
(2)设点![]() ,根据
,根据![]() ,可得关于m的方程,解方程即可求解;
,可得关于m的方程,解方程即可求解;
(3)分三种情况:①当![]() ,∠QMN=90°时,②当
,∠QMN=90°时,②当![]() ,∠QNM=90°时,③当
,∠QNM=90°时,③当![]() ,∠NQM=90°时,分别根据等腰直角三角形的性质列出方程求解即可.
,∠NQM=90°时,分别根据等腰直角三角形的性质列出方程求解即可.
解:(1)联立![]() 与
与![]() 得:
得:![]() ,
,![]()
∴![]()
(2)设![]()
∵直线![]() 的解析式为
的解析式为![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,
,
∴点C(6,0),OC=6,
∴![]() ,即
,即![]()
解得:![]() 或
或![]() ,
,
∴点![]() 的坐标为:
的坐标为:![]() 或
或![]() ;
;
(3)存在,
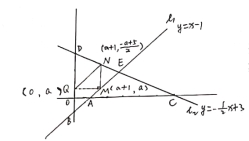
分三种情况:①当![]() ,∠QMN=90°时,
,∠QMN=90°时,
设点Q的坐标为(0,a),则M的坐标为(a+1,a)、N的坐标为(a+1,![]() ),
),
∴![]()
解得:![]() ,
,
∴![]() ;
;
②当![]() ,∠QNM=90°时,
,∠QNM=90°时,
设点Q的坐标为(0,b),则N的坐标为(6-2b,b),M的坐标为(6-2b,5-2b),
∴![]() ,
,
解得:![]() ,
,
∴![]() ;
;

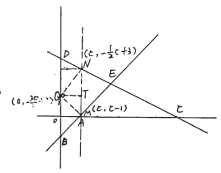
③当![]() ,∠NQM=90°时,
,∠NQM=90°时,
设点N的坐标为(c,![]() ),则M的坐标为(c,c-1),
),则M的坐标为(c,c-1),
过![]() 作
作![]() ,则QT=TM=c,
,则QT=TM=c,
∴点Q的坐标为(0,2c-1),
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.
综上,满足条件的所有点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和
和![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”.
的“二次对称点”.
(1)已知点![]() ,直线
,直线![]() 是经过
是经过![]() 且平行于
且平行于![]() 轴的一条直线,则点
轴的一条直线,则点![]() 的“二次对称点”的坐标为______;
的“二次对称点”的坐标为______;
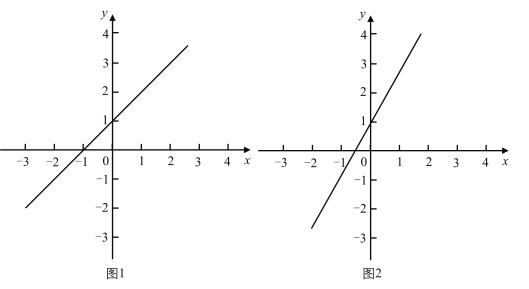
(2)如图1,直线![]() 经过
经过![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
①点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”的坐标为______;
的“二次对称点”的坐标为______;
②当点![]() 在
在![]() 轴上移动,请你在图1中画出它关于
轴上移动,请你在图1中画出它关于![]() 轴,直线
轴,直线![]() 的“二次对称点”的运动路径.
的“二次对称点”的运动路径.
(3)如图2,![]() 是
是![]() 轴上的动点,线段
轴上的动点,线段![]() 经过点
经过点![]() ,且点
,且点![]() 点
点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 经过
经过![]() 且与
且与![]() 轴负半轴夹角为60°,在点
轴负半轴夹角为60°,在点![]() 的运动过程中,若线段
的运动过程中,若线段![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”,且点
的“二次对称点”,且点![]() 在
在![]() 轴上,则点
轴上,则点![]() 的纵坐标
的纵坐标![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
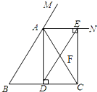
![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是一个正方形?并给出证明.
是一个正方形?并给出证明.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求正方形
,求正方形![]() 周长.
周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】举重比赛的总成绩是选手的挺举与抓举两项成绩之和,若其中一项三次挑战失败,则该项成绩为 0,甲、乙是同一重量级别的举重选手,他们近三年六次重要比赛的成绩如下(单位:公斤):
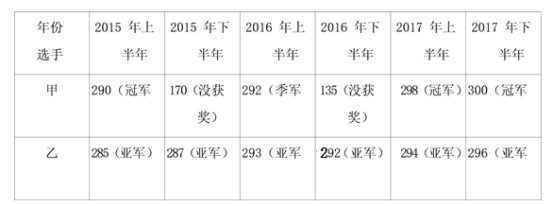
如果你是教练,要选派一名选手参加国际比赛,那么你会选择_____(填“甲” 或“乙”),理由是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着高铁的建设,春运期间动车组发送旅客量越来越大,相关部门为了进一步了解春运期间动车组发送旅客量的变化情况,针对2014年至2018年春运期间的铁路发送旅客量情况进行了调查,过程如下.
(Ⅰ)收集、整理数据
请将表格补充完整:
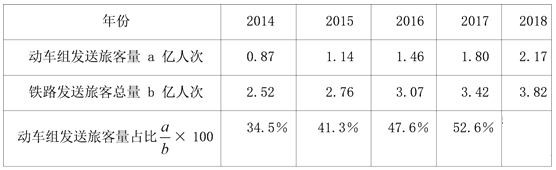
(Ⅱ)描述数据
为了更直观地显示动车组发送旅客量占比的变化趋势,需要用什么图(回答“折线图”或“扇形图”)进行描述;
(Ⅲ)分析数据、做出推测
预估2019年春运期间动车组发送旅客量占比约为多少,说明你的预估理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )

A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与正比例函数
的图像与正比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像都经过
)的图像都经过![]() .
.
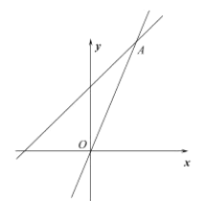
(1)求点![]() 的坐标及正比例函数的表达式;
的坐标及正比例函数的表达式;
(2)利用函数图像比较![]() 和
和![]() 的大小并直接写出对应的
的大小并直接写出对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com