
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和
和![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”.
的“二次对称点”.
(1)已知点![]() ,直线
,直线![]() 是经过
是经过![]() 且平行于
且平行于![]() 轴的一条直线,则点
轴的一条直线,则点![]() 的“二次对称点”的坐标为______;
的“二次对称点”的坐标为______;
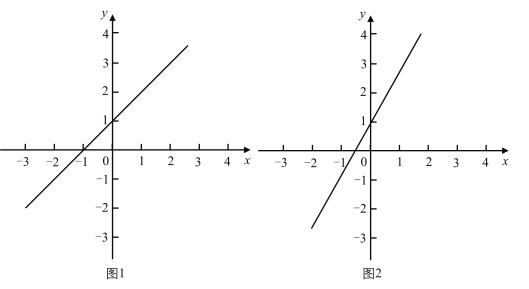
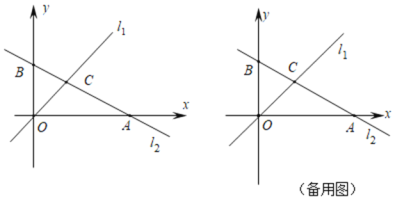
(2)如图1,直线![]() 经过
经过![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
①点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”的坐标为______;
的“二次对称点”的坐标为______;
②当点![]() 在
在![]() 轴上移动,请你在图1中画出它关于
轴上移动,请你在图1中画出它关于![]() 轴,直线
轴,直线![]() 的“二次对称点”的运动路径.
的“二次对称点”的运动路径.
(3)如图2,![]() 是
是![]() 轴上的动点,线段
轴上的动点,线段![]() 经过点
经过点![]() ,且点
,且点![]() 点
点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 经过
经过![]() 且与
且与![]() 轴负半轴夹角为60°,在点
轴负半轴夹角为60°,在点![]() 的运动过程中,若线段
的运动过程中,若线段![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”,且点
的“二次对称点”,且点![]() 在
在![]() 轴上,则点
轴上,则点![]() 的纵坐标
的纵坐标![]() 的取值范围是_____.
的取值范围是_____.
【答案】(1)(1,4);(2)①(-1,-1);②见解析;(3)-3<![]() <1
<1
【解析】
(1)根据“二次对称点”的概念先算出A关于y轴对称点,再求出该点关于l的点即可;
(2)①求出直线l的解析式,从而根据定义得出结果;
②根据对称的性质可得运动路径是直线,从而求出该直线,画出即可;
(3)根据题意讨论当点N分别与点R和点S重合时,求出点N′的运动路径,再根据点N′在线段RS上得出![]() 的最大值和最小值即可.
的最大值和最小值即可.
解:(1)由题意可知:∵A(-1,0),
∴点A关于y轴对称的点A1坐标为(1,0),
∵l是经过(0,2)且平行于![]() 轴的一条直线,即y=2,
轴的一条直线,即y=2,
∴点A关于![]() 轴,直线
轴,直线![]() 的“二次对称点”坐标为(1,4);
的“二次对称点”坐标为(1,4);
(2)①∵直线![]() 经过
经过![]() 、
、![]() ,
,
设直线l的解析式为y=kx+b,将![]() 、
、![]() ,代入
,代入
![]() ,
,
解得![]() ,
,
∴直线l的解析式为:y=x+1,
∵点E(2,0),
由题意可得点E关于![]() 轴,直线
轴,直线![]() 的“二次对称点”为(-1,-1);
的“二次对称点”为(-1,-1);
②由关于![]() 轴,直线
轴,直线![]() 的“二次对称点”的定义可知,
的“二次对称点”的定义可知,
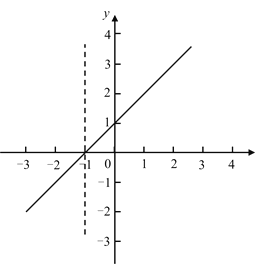
当点E在x轴运动时,点E关于y轴对称的点E1也在x轴上,
而点x轴关于直线l的对称图形为直线x=-1,
∴点E1关于直线l对称点在直线x=-1上,运动轨迹如图:
(3)∵直线![]() 经过
经过![]() 且与
且与![]() 轴正半轴夹角为60°,
轴正半轴夹角为60°,
如图,直线l与x轴交于点C,与y轴交于点B,
∴∠BCO=60°,
∴BC=2CO,
在△BCO中,BO2+CO2=BC2,BO=1,
解得:CO=![]() ,即点C(
,即点C(![]() ,0),
,0),
结合B(0,1),可求得:直线l的表达式:![]() ,
,
当点N与点R重合, N(t,1),
由题意可知,如图,此时点N′的运动路径为l1,
∵∠CBO=90°-60°=30°,
∴∠N″BO=30°,
∵OB=1,
∴可知l1和l关于y轴对称,
∴l1的表达式为:y=![]() ,
,
与y轴交点为(0,1);
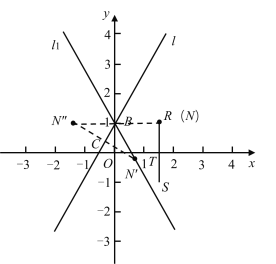
当点N和点S重合,N(t,-1),
由题意可知,如图,此时点N′的运动路径为l2,且l1∥l2,
设l2的解析式为y=![]() x+b1,
x+b1,
当N′在l1上时,将y=-1代入l1,
解得x=![]() ,
,
此时N′坐标为(![]() ,-1),代入l2中,
,-1),代入l2中,
解得b1=-3,
∴l2的解析式为y=![]() x-3,
x-3,
∴l2与y轴交点为(0,-3),
由题意可知当点N在线段RS上时,N′的运动轨迹皆为直线,且在l1和l2之间,
综上所述,![]() 的取值范围是:-3<
的取值范围是:-3<![]() <1.
<1.



科目:初中数学 来源: 题型:
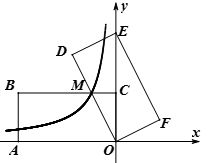
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如![]() 就是一个“中高数”.若十位上数字为
就是一个“中高数”.若十位上数字为![]() ,则从
,则从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中任选两个不同的数,与
中任选两个不同的数,与![]() 组成“中高数”的概率是________.
组成“中高数”的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机摸出一个小球,记录下数字后放回,再随机摸出一个小球.
(1)请用树状图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出球上的数字的积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,BC=6 cm,AC=8 cm,点P从点A开始沿AC向点C以2厘米/秒的速度运动;与此同时,点Q从点C开始沿CB边向点B以1厘米/秒的速度运动;如果P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动.
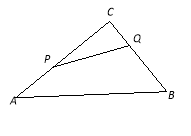
(1)经过几秒,△CPQ的面积等于3cm2?
(2)在整个运动过程中,是否存在某一时刻t,使PQ恰好平分△ABC的面积?若存在,求出运动时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,请求出点
,请求出点![]() 的坐标;
的坐标;
(3)在![]() 轴右侧、点
轴右侧、点![]() 左侧有一条平行于
左侧有一条平行于![]() 轴的动直线,分别与
轴的动直线,分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰直角三角形?若存在,请求出满足条件的所有点
为等腰直角三角形?若存在,请求出满足条件的所有点![]() 的坐标;若不存在;请说明理由.
的坐标;若不存在;请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了美化绿化校园,计划购买甲,乙两种花木共100棵绿化操场,其中甲种花木每棵60元,乙种花木每棵80元.
(1)若购买甲,乙两种花木刚好用去7200元,则购买了甲,乙两种花木各多少棵?
(2)如果购买乙种花木的数量不少于甲种花木的数量,请设计一种购买方案使所需费用最低,并求出该购买方案所需总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com