
【题目】某学校为了美化绿化校园,计划购买甲,乙两种花木共100棵绿化操场,其中甲种花木每棵60元,乙种花木每棵80元.
(1)若购买甲,乙两种花木刚好用去7200元,则购买了甲,乙两种花木各多少棵?
(2)如果购买乙种花木的数量不少于甲种花木的数量,请设计一种购买方案使所需费用最低,并求出该购买方案所需总费用.
【答案】(1)购买甲种花木40棵,乙种花木60棵;(2)当购买甲种花木50棵,乙种花木50棵是所需费用最低,费用为7000元.
【解析】
(1)设购买甲种花木x棵,乙种花木y棵,根据题意可以列出相应的二元一次方程组,解方程组求出x、y的值即可得答案;
(2)设购买甲种花木a棵,则购买乙种花木(100﹣a)棵,所需费用为w元,根据题意可以得到费用与甲种花木数量的函数关系式,然后根据购买乙种花木的数量不少于甲种花木的数量,可以得到购买甲种花木的数量的取值范围,再根据一次函数的性质即可解答本题.
(1)设购买甲种花木x棵,乙种花木y棵,
∵购买甲,乙两种花木共100棵,刚好用去7200元,
∴![]() ,
,
解得:![]() ,
,
答:购买甲种花木40棵,乙种花木60棵;
(2)设购买甲种花木a棵,则购买乙种花木(100﹣a)棵,所需费用为w元,
w=60a+80(100﹣a)=﹣20a+8000,
∵购买乙种花木的数量不少于甲种花木的数量,
∴a≤100﹣a,
解得,a≤50,
∵-20<0,
∴w随a的增大而减小,
∴当a=50时,w取得最小值,此时w=﹣20×50+8000=7000,100﹣a=50,
答:当购买甲种花木50棵,乙种花木50棵是所需费用最低,费用为7000元.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和
和![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”.
的“二次对称点”.
(1)已知点![]() ,直线
,直线![]() 是经过
是经过![]() 且平行于
且平行于![]() 轴的一条直线,则点
轴的一条直线,则点![]() 的“二次对称点”的坐标为______;
的“二次对称点”的坐标为______;
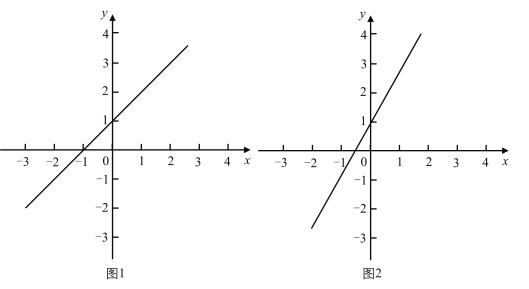
(2)如图1,直线![]() 经过
经过![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
①点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”的坐标为______;
的“二次对称点”的坐标为______;
②当点![]() 在
在![]() 轴上移动,请你在图1中画出它关于
轴上移动,请你在图1中画出它关于![]() 轴,直线
轴,直线![]() 的“二次对称点”的运动路径.
的“二次对称点”的运动路径.
(3)如图2,![]() 是
是![]() 轴上的动点,线段
轴上的动点,线段![]() 经过点
经过点![]() ,且点
,且点![]() 点
点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 经过
经过![]() 且与
且与![]() 轴负半轴夹角为60°,在点
轴负半轴夹角为60°,在点![]() 的运动过程中,若线段
的运动过程中,若线段![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的“二次对称点”,且点
的“二次对称点”,且点![]() 在
在![]() 轴上,则点
轴上,则点![]() 的纵坐标
的纵坐标![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )

A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
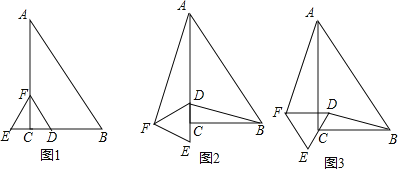
【题目】△ABC中,∠ACB=90°,∠BAC=30°,点C为等边△DEF的边DE的中点.
(1)如图1,当DE与BC在同一条直线上时,已知![]() ,求
,求![]() 的值;
的值;
(2)如图2,当DE与AC在同一条直线上时,分别连接AF,BD,试判断BD和AF的位置关系并说明理由;
(3)如图3,当DE与△ABC的边均不在一条直线上时,分别连接AF,BD,求证:∠FAC=∠CBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与正比例函数
的图像与正比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像都经过
)的图像都经过![]() .
.
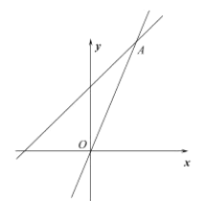
(1)求点![]() 的坐标及正比例函数的表达式;
的坐标及正比例函数的表达式;
(2)利用函数图像比较![]() 和
和![]() 的大小并直接写出对应的
的大小并直接写出对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com