
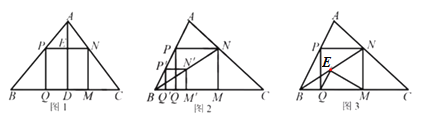
����Ŀ��С���ڸ�ϰʱ������һ���α��ϵ����⣬�¹ʺ�����˲�������������չ��
(1)�¹ʣ���ͼ1������ABC�У�AD��BC�ڵ�D��������PQMN�ı�QM��BC�ϣ�����P��N�ֱ���AB�� AC�ϣ���BC=6��AD=4����������PQMN�ı߳���
(2)�������ܻ���������������?С������ѧ�Ҳ������ڡ��������⡷�еķ������в�������ͼ2�����⻭��ABC����AB����ȡһ��P������������P��Q��M��N����ʹQ��,M����BC���ϣ�N������ABC�ڣ�����B N�����ӳ���AC�ڵ�N����NM��BC�ڵ�M��NP��NM��AB�ڵ�P��PQ��BC�ڵ�Q���õ��ı���PQMN��С�����߶�BN��Ϊ��������������
(3)������֤��ͼ2�е��ı���PQMN �������Σ�
(4)��չ����(2)�������£��ڲ���ҵ��B N�Ͻ�ȡNE=NM������EQ��EM(��ͼ3)����tan��NBM=![]() ʱ�������QEM�Ķ�����������֤����
ʱ�������QEM�Ķ�����������֤����
�����С��������¹�������������������չ���е����⣮
���𰸡���1���¹ʣ�![]() ����3���������ı���PQMNΪ������.����������4����չ������
����3���������ı���PQMNΪ������.����������4����չ������![]() �����ɼ�����.
�����ɼ�����.
��������
��1������![]() ���б���ʽ��⼴�ɣ�
���б���ʽ��⼴�ɣ�
��3��������֪�ı���PQMNΪ���Σ�ͨ������������֤��![]() ,
,![]() ,�Ӷ�
,�Ӷ�![]() ����֤�ı���PQMNΪ�����Σ�
����֤�ı���PQMNΪ�����Σ�
��4��![]() ����MN=3k��
����MN=3k��![]() .��
.��![]() ��
��![]() ��
��![]() .�������߶�Ӧ�ɱ����Ҽн���ȿ�֤
.�������߶�Ӧ�ɱ����Ҽн���ȿ�֤![]() ���Ӷ�
���Ӷ�![]() .ͨ��֤��
.ͨ��֤��![]() ���ɵ�
���ɵ�![]() .
.
��1���¹ʣ�![]() ��
��
![]() .
.
![]() ��
��![]() .
.
���![]() .
.
��2���������ɻ����ɵ�![]() .
.
![]() �ı���PQMNΪ���Σ�
�ı���PQMNΪ���Σ�![]() .
.
![]() ��
��
![]()
ͬ���ɵ�![]() .
.
![]() .
.
![]() ��
��![]() .
.
![]() �ı���PQMNΪ������.
�ı���PQMNΪ������.
��3����չ������![]() ���������£�
���������£�
��![]() ����MN=3k��
����MN=3k��![]() .
.
��![]() ��
��![]() ��
��![]() .
.
![]() ��
��![]() ��
��
![]() .
.
![]() ��
��
![]() ��
��
![]() .
.
![]() ��
��
![]() .
.
![]() ��
��
![]() .
.
![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��PM2.5��ָ������ֱ��С�ڻ����2.5��m��0.0000025m���Ŀ�������д����ж����к����ʣ�Ҳ�ƿ���ο������0.0000025�ÿ�ѧ��������ʾΪ
A.25��10��7B.2.5��10��6C.0.25��10��5D.2.5��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:![]() ��
��![]() ���ڽ�������,��
���ڽ�������,��![]() ,ֱ��
,ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() .
.
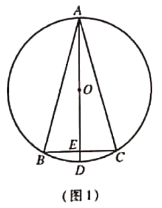
![]() ��ͼ1 ,��֤��
��ͼ1 ,��֤��![]() ��
��
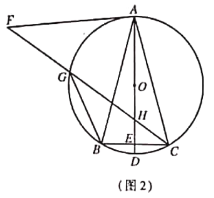
![]() ��ͼ2,���߶�
��ͼ2,���߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�õ��߶�
˳ʱ����ת�õ��߶�![]() ,��ת��Ϊ
,��ת��Ϊ![]() ����
����![]() �ֱ�
�ֱ�![]() ,
,![]() �ڵ�
�ڵ�![]() ,����
,����![]() ,��֤:
,��֤: ![]() ��
��
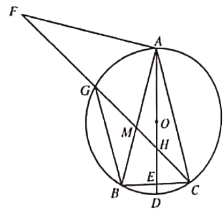
![]() ��ͼ3,��(2)��������,��
��ͼ3,��(2)��������,��![]() ʱ,
ʱ,![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
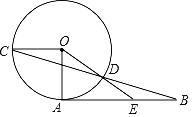
����Ŀ����ͼ��AB����O�����ߣ�OA��OC����O�İ뾶����OC��AB������BC����O�ڵ�D����DǡΪBC���е㣬����OD���ӳ�����AB�ڵ�E��
��1�����B�Ķ�����
��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
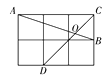
����Ŀ����ͼ���ڱ߳�Ϊ1��С�����������У���A��B��C��D������ЩС�����εĶ����ϣ�AB��CD�ཻ�ڵ�O����tan��AOD=________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����![]() Ԫ�ļ۸�һ��������������ۣ���۾ָ����г�����涨�����۵��۲�����
Ԫ�ļ۸�һ��������������ۣ���۾ָ����г�����涨�����۵��۲�����![]() Ԫ�Ҳ�����
Ԫ�Ҳ�����![]() Ԫ���������з��֣��ÿ������ÿ����������
Ԫ���������з��֣��ÿ������ÿ����������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮�����ij�ֺ�����ϵ����Ӧ���£�
��Ԫ��֮�����ij�ֺ�����ϵ����Ӧ���£�
���۵��� |
|
|
|
|
|
�������� |
|
|
|
|
|
��1��������ѧ���ĺ���֪ʶ�����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2�����ʸÿ�����ÿ������![]() ��Ԫ�������ֵ�Ƕ��٣�
��Ԫ�������ֵ�Ƕ��٣�
��3������ÿ�����ÿ��������벻����![]() Ԫ�������ÿ����������
Ԫ�������ÿ����������![]() ����Ϊ���ٱ���
����Ϊ���ٱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
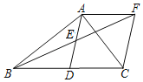
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������
������![]() ��
��
��֤����1��![]() ��
��![]() ��
��
��2���ı���![]() �����Σ�
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
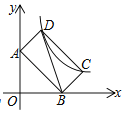
����Ŀ����ͼ������ABCD�ı�AB�Ľ���ʽΪy��ax+2������C��D��˫����y��![]() ��k��0���ϣ���AB��2AD����k��_____��
��k��0���ϣ���AB��2AD����k��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() ��y�ύ�ڵ�
��y�ύ�ڵ�![]() ��
��
��1����c��ֵ��
��2����![]() ʱ���������߶�������ꣻ
ʱ���������߶�������ꣻ
��3����֪��![]() ����������
����������![]() ���߶�
���߶�![]() �����������㣬��Ϻ���ͼ����a��ȡֵ��Χ��
�����������㣬��Ϻ���ͼ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com