
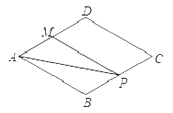
【题目】如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
A. 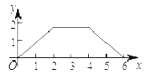 B.
B. 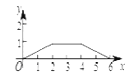 C.
C. 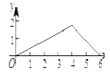 D.
D. 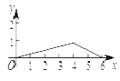
【答案】A
【解析】
分类讨论:当0≤x≤2,如图1,作PH⊥AD于H,AP=x,根据菱形的性质得∠A=60°,AM=1,则∠APH=30°,根据含30度的直角三角形三边的关系得到在RtAH=![]() x,PH=
x,PH=![]() x,然后根据三角形面积公式得y=
x,然后根据三角形面积公式得y=![]() AMPH=
AMPH=![]() x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=1,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=
x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=1,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=![]() ,然后根据三角形面积公式得y=
,然后根据三角形面积公式得y=![]() AMBE=
AMBE=![]() ;
;
当4<x≤6,如图3,作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,根据菱形的性质得∠ADC=120°,则∠DPF=30°,在Rt△DPF中,根据含30度的直角三角形三边的关系得DF=![]() (6-x),PF=
(6-x),PF=![]() DF=
DF=![]() (6-x),则利用三角形面积公式得y=
(6-x),则利用三角形面积公式得y=![]() AMPF=-
AMPF=-![]() x+
x+![]() ,最后根据三个解析式和对应的取值范围对各选项进行判断.
,最后根据三个解析式和对应的取值范围对各选项进行判断.
当点P在AB上运动时,即0≤x≤2,如图1,
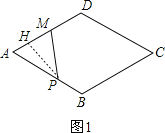
作PH⊥AD于H,AP=x,
∵菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,
∴∠A=60°,AM=1,
∴∠APH=30°,
在Rt△APH中,AH=![]() AP=
AP=![]() x,
x,
PH=![]() AH=
AH=![]() x,
x,
∴y=![]() AMPH=
AMPH=![]() ×1×
×1×![]() x=
x=![]() x;
x;
当点P在BC上运动时,即2<x≤4,如图2,
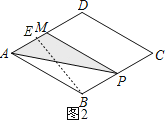
作BE⊥AD于E,AP+BP=x,
∵四边形ABCD为菱形,∠B=120°,
∴∠A=60°,AM=1,AB=2,BC∥AD,
∴∠ABE=30°,
在Rt△ABE中,AE=![]() AB=1,
AB=1,
PH=![]() AE=
AE=![]() ,
,
∴y=![]() AMBE=
AMBE=![]() ×1×
×1×![]() =
=![]() ;
;
当点P在CD上运动时,即4<x≤6,如图3,
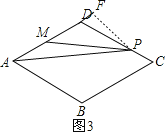
作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,
∵菱形ABCD中,∠B=120°,
∴∠ADC=120°,
∴∠DPF=30°,
在Rt△DPF中,DF=![]() DP=
DP=![]() (6-x),
(6-x),
PF=![]() DF=
DF=![]() (6-x),
(6-x),
∴y=![]() AMPF=
AMPF=![]() ×1×
×1×![]() (6-x)=
(6-x)=![]() (6-x)=-
(6-x)=-![]() x+
x+![]() ,
,
∴△APM的面积y与点P经过的路程x之间的函数关系的图象为三段:当0≤x≤2,图象为线段,满足解析式y=![]() x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为
x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为![]() ;当4≤x≤6,图象为线段,且满足解析式y=-
;当4≤x≤6,图象为线段,且满足解析式y=-![]() x+
x+![]() .
.
故选B.


科目:初中数学 来源: 题型:
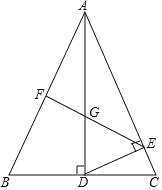
【题目】如图,在△ABC中.AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连EF交AD于点G.
(1)求证:AD2=ABAE;
(2)若AB=3,AE=2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
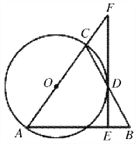
【题目】如图,在△ABC中,AB=AC,以AC为直径作![]() 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证: EF与![]() 相切;
相切;
(2)若AE=6,![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )
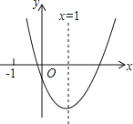
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在矩形ABCD中,AB=3,AD=4,点P为AB边上的动点(P与A、B不重合),将△BCP沿CP翻折,点B的对应点B1在矩形外,PB1交AD于E,CB1交AD于点F.
(1)如图1,求证:△APE∽△DFC;
(2)如图1,如果EF=PE,求BP的长;
(3)如图2,连接BB′交AD于点Q,EQ:QF=8:5,求tan∠PCB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.
(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)
(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)
(测倾器的高度忽略不计,参考数据:tan53°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)

查看答案和解析>>
科目:初中数学 来源: 题型:
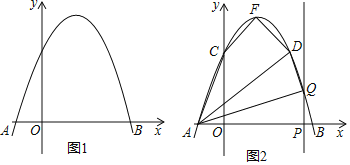
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com