
分析 根据|1-$\sqrt{(x-1)^{2}}$|=x,进行分类情况讨论解答.
解答 解;当≥2时,|1-$\sqrt{(x-1)^{2}}$|=x-2≠x,
当1<x<2时,|1-$\sqrt{(x-1)^{2}}$|=2-x<1,
∴|1-$\sqrt{(x-1)^{2}}$|≠x,
∴x≤1,
又x=|1-$\sqrt{(x-1)^{2}}$|≥0,
∴0≤x≤1,
∴原式=$\sqrt{(x-\frac{1}{2})^{2}}+\sqrt{(x+\frac{1}{2})^{2}}$=|x-$\frac{1}{2}$|+|x+$\frac{1}{2}$|,
∴①当$0≤x<\frac{1}{2}$时,原式=($\frac{1}{2}$-x)+(x+$\frac{1}{2}$)=1,
②当$\frac{1}{2}≤x≤1$时,原式=(x-$\frac{1}{2}$)+(x+$\frac{1}{2}$)=2x.
点评 本题考查了二次根式的性质与化简,解决本题的关键是进行分类讨论.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
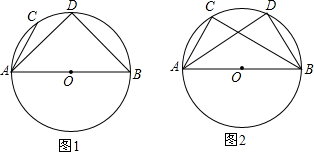
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com