练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

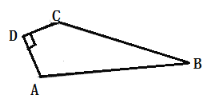
    【题目】如图，所是一块草坪已知：AD=12m，CD=9m，∠ADC=90°，AB=39m， BC=36m，求这块草坪的面积.

    【答案】324m2

    【解析】

    连接AC，根据直角△ACD可以求得斜边AC的长度，根据AC，BC，AB可以判定△ABC为直角三角形，要求这块地的面积，求△ABC与△ACD的面积之和即可．

    解：连接AC，

    已知，在直角△ACD中，CD=9m，AD=12m，

    根据AD2+CD2=AC2，可以求得AC=15m，

    在△ABC中，AB=39m，BC=36m，AC=15m，

    ∴存在AC2+CB2=AB2，

    ∴△ABC为直角三角形，

    要求这块地的面积，求△ABC和△ACD的面积之差即可，

    S=S△ABC+S△ACD

    ，

    ，

    =270+54，

    =324（m2），

    答：这块地的面积为324m2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】鸡兔同笼问题是我国古代著名趣题之一，大约在 1500 年前，《孙子算经》中就记载了这个有趣的问题．书中是这样叙述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡、兔同在一个笼子里，从上上面数，有 35 个头；从下面数，有 94 只脚 ．求笼中各有几只鸡和兔？经计算可得（ ）

    A. 鸡 20 只，兔 15 只 B. 鸡 12 只，兔 23 只

    C. 鸡 15 只，兔 20 只 D. 鸡 23 只，兔 12 只

    查看答案和解析>>

    科目：初中数学 来源： 题型：

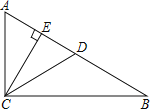
    【题目】在直角三角形ABC中，∠ACB=90°，D、E是边AB上两点，且CE所在直线垂直平分线段AD，CD平分∠BCE，BC=2，则AB=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】邮递员骑摩托车从邮局出发，先向东骑行2km到达A村，继续向东骑行3km到达B村，然后向西骑行9km到C村，最后回到邮局．

    （1）以邮局为原点，以向东方向为正方向，用1个单位长度表示1km，请你在数轴上表示出A、B、C三个村庄的位置；

    （2）C村离A村有多远？

    （3）若摩托车每1km耗油0.03升，这趟路共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题情境）学习《探索全等三角形条件》后，老师提出了如下问题：如图①，△ABC中，若AB=12，AC=8，求BC边上的中线AD的取值范围。同学通过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，连接BE.根据SAS可证得到△ADC≌△EDB，从而根据“三角形的三边关系”可求得AD的取值范围是 。解后反思：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.

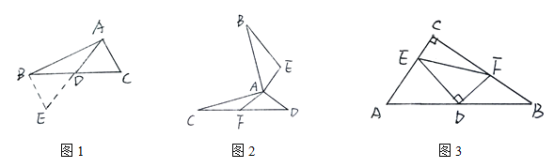
    （直接运用）如图②，AB⊥AC，AD⊥AE，AB=AC，AD=AE，AF是ACD的边CD上中线.求证：BE=2AF.

    （灵活运用）如图③，在△ABC中，∠C=90°，D为AB的中点，DE⊥DF，DE交AC于点E，DF交AB于点F，连接EF，试判断以线段AE、BF、EF为边的三角形形状，并证明你的结论.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AF⊥BD于E，AF交BC于点F,连接DF,下列结论：①△ABD≌△CDB；②∠BFE=∠BDC；③S△ABE=S△DEF；④AB=6,AD=8,DB=10，则AE=4.其中正确的个数为（ ）

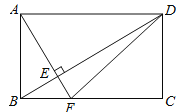
    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

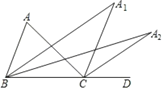
    【题目】如图，∠ACD是△ABC的外角，∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2，∠A2BC的平分线与∠A2CD的平分线交于点A3.设∠A=64°.则（1）∠A1=________；（2）∠A3=_______。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地电话拨号上网有两种收费方式，用户可以任意选择其中一种：第一种是计时制，0.05元／分； 第二种是包月制，69元／月（限一部个人住宅电话上网）．此外，每一种上网方式都得加收通讯费0.02元／分．

    （1）若小明家今年三月份上网的时间为小时，请你分别写出两种收费方式下小明家应该支付的费用；

    （2）若小明估计自家一个月内上网的时间为20小时，你认为采用哪种方式较为合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等．

    …

    （1）可求得 ，第个格子中的数为 ；

    （2）若前个格子中所填整数之和，则的值为多少？若的值为多少？

    （3）若，则的最小值为 ．

    查看答案和解析>>

    同步练习册答案