

 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
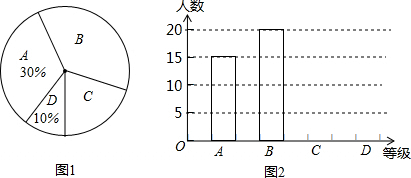
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,秋千链子AB的长度为3m,静止时的秋千踏板(厚度忽略不计)距地面DE为0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为53°,求秋千踏板与地面的最大距离.(sin53°≈0.80,cos53°≈0.60)
如图,秋千链子AB的长度为3m,静止时的秋千踏板(厚度忽略不计)距地面DE为0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为53°,求秋千踏板与地面的最大距离.(sin53°≈0.80,cos53°≈0.60)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-(x-1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线另一点D,连结AC,DE∥AC交边CB于点E.
如图,抛物线y=-(x-1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线另一点D,连结AC,DE∥AC交边CB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com