练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某船向正东航行，在A处望见灯塔C在东北方向，前进到B处望见灯塔C在北偏西30°，又航行了半小时到D处，望见灯塔C恰在西北方向，若船速为每小时20海里．求A、D两点间的距离．（结果不取近似值）

    【答案】解：作CH⊥AD于点H，
    由题意可得：△ACD是等腰直角三角形，则CH= AD，设CH=x，则DH=x，
    在Rt△CBH中，∠BCH=30°，
    则 =tan30°，故BH= x，
    ∴BD=x﹣ x= ×20，
    解得：x=15+5 ，
    故2x=30+10 ．
    答：A、D两点间的距离为（30+10 ）海里．

    【解析】先作CH⊥AD，可得BD= ×20，AH=DH，可求AH的长，从而求得AD的长．
    【考点精析】关于本题考查的关于方向角问题，需要了解指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

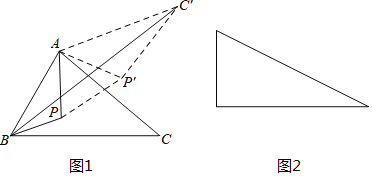
    【题目】问题的提出：如果点P是锐角内一动点，如何确定一个位置，使点P到的三顶点的距离之和的值为最小？

    问题的转化：把绕点A逆时针旋转得到，连接，这样就把确定的最小值的问题转化成确定的最小值的问题了，请你利用图1证明：；

    问题的解决：当点P到锐角的三顶点的距离之和的值为最小时，求和的度数；

    问题的延伸：如图2是有一个锐角为的直角三角形，如果斜边为2，点P是这个三角形内一动点，请你利用以上方法，求点P到这个三角形各顶点的距离之和的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列方程组：

    （1）

    （2）

    （3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以直线AB上一点O为端点作射线 OC，使∠BOC=60°，将一个直角三角形的直角顶点放在点O处．（注：∠DOE=90°）

    （1）如图1，若直角三角板DOE的一边OD放在射线OB上，则∠COE= °；

    （2）如图2，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OE恰好平分∠AOC，请说明OD所在射线是∠BOC的平分线；

    （3）如图3，将三角板DOE绕点O逆时针转动到某个位置时，若恰好∠COD= ∠AOE，求∠BOD的度数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，然后解答后面的问题．

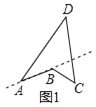
    （1）定义：把四边形的某些边向两方延长，其他各边有不在延长所得直线的同一旁，这样的四边形叫做凹四边形．如图1，四边形ABCD为凹四边形．

    （2）性质探究：请完成凹四边形一个性质的证明．

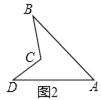
    已知：如图2，四边形ABCD是凹四边形．

    求证：∠BCD=∠B+∠A+∠D．

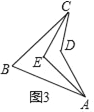
    （3）性质应用：

    如图3，在凹四边形ABCD中，∠BAD的角平分线与∠BCD的角平分线交于点E，若∠ADC=140°，∠AEC=102°，则∠B=_____°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有理数a,b,c在数轴上的对应点如图所示.

    （1）在横线上填上“＞”或“＝”或“＜”：

    a 0,a-b 0,.

    （2）在数轴上标出表示有理数-a,-b,-c的点；

    （3）用“＞”把a,b,c,-a,-b,-c连接起来.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx﹣3的图象与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．该抛物线的顶点为M．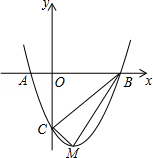

    （1）求该抛物线的解析式；
    （2）判断△BCM的形状，并说明理由．
    （3）探究坐标轴上是否存在点P，使得以点P，A，C为顶点的三角形与△BCM相似？若存在，请求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个圆锥的侧面积是它底面积的2倍，则这个圆锥的侧面展开图的圆心角是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“农民也可以报销医疗费了！”这是某市推行新型农村医疗合作的成果．村民只要每人每年交10元钱，就可以加入合作医疗，每年先由自己支付医疗费，年终时可得到按一定比例返回的返回款．这一举措极大地增强了农民抵御大病风险的能力．小华与同学随机调查了他们乡的一些农民，根据收集到的数据绘制了以下的统计图．
    根据以上信息，解答以下问题：
    （1）本次调查了多少村民，被调查的村民中，有多少人参加合作医疗得到了返回款；
    （2）该乡若有10 000村民，请你估计有多少人参加了合作医疗？要使两年后参加合作医疗的人数增加到9 680人，假设这两年的年增长率相同，求这个年增长率．

    查看答案和解析>>

    同步练习册答案