Question

中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯．在雷达显示图上，标明了三艘海监船的坐标为O（0，0）、B（80，0）、C（80，60），（单位：海里）三艘海监船安装有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域（只考虑在海平面上的探测）．

（1）若在三艘海监船组成的△OBC区域内没有探测盲点，则雷达的有效探测半径r至少为_______海里；

（2）某时刻海面上出现一艘菲律宾海警船A，在海监船C测得点A位于南偏东60°方向上，同时在海监船B测得A位于北偏东45°方向上，海警船A正以每小时20海里的速度向正西方向移动，我海监船B立刻向北偏东15°方向运动进行拦截，问我海监船B至少以多少速度才能在此方向上拦截到菲律宾海警船A？

 

 

Answer 1

【解析】

试题分析：（1）利用点的坐标性质得出CO的长，进而利用直角三角形外心的性质得出答案；

（2）利用方向角画出图形，进而利用锐角三角角函数关系得出即可．

试题解析：（1）∵O（0，0）、B（80，0）、C（80，60），

∴BO=80，BC=60，且∠OBC=90°，

∴CO=，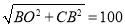

当雷达在CO的中点位置时，正好位于△BCO外心的位置，

此时在三艘海监船组成的△OBC区域内没有探测盲点，雷达的有效探测半径r至少为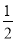CO=50（海里）；

（2）过点A作AD⊥BC于点D，

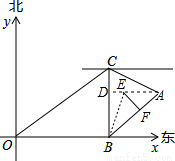
设BD=x，由题意得：AD=BD=x，

则tan60°=，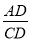

∴CD=，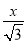

∴x+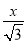=60，

解得：x=90-30，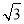

设船和舰在点E处相遇，海监船的速度为v海里/小时，过点E作EF⊥AB于点F，设AF=y，由题意得：

AE=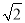y，BE=2y，

∴，

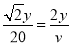解得：v=20，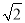

答：我海监船B至少以20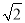海里/小时速度才能在此方向上拦截到菲律宾海警船A．

考点：解直角三角形的应用-方向角问题．