
如图,直角梯形OABC中,AB∥OC,点A坐标为(0,6),点C坐标为(3,0),BC= ,一抛物线过点A、B、 C.
,一抛物线过点A、B、 C.
(1)填空:点B的坐标为 ;
(2)求该抛物线的解析式;
(3)作平行于x轴的直线与x轴上方的抛物线交于点E 、F,以EF为直径的圆恰好与x轴相切,求该圆的半径.

(1)(4,6).(2)y=2x2-8x+6.(3)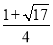 .
.
【解析】
试题分析:(1)可设点B的坐标为(a,6),根据两点间的距离公式即可得到关于a的方程,解方程求得a的值,进一步得到点B的坐标.
(2)已知抛物线过A,B,C三点,可根据三点的坐标用待定系数法求出抛物线的解析式.
(3)设以线段EF为直径的圆的半径为r,那么可用半径r表示出E,F两点的坐标,然后根据E,F在抛物线上,将E,F的坐标代入抛物线的解析式中,可得出关于r的方程,解方程即可得出的r的值.
(1)设点B的坐标为(a,6),依题意有
(a-3)2+62=(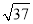 )2,
)2,
解得a1=4,a2=2(不合题意舍去),
故点B的坐标为(4,6).
(2)令抛物线的解析式为y=ax2+bx+c,
则 ,
,
解得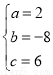 ,
,
∴抛物线的解析式为y=2x2-8x+6.
(3)抛物线对称轴为x=2,
设E的坐标为(2-r,r),则F的坐标为(2+r,r),
而E点在抛物线y=2x2-8x+6上,
∴r=2(2-r)2-8(2-r)+6;
解得r1=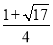 ,r2=
,r2=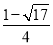 (舍去);
(舍去);
故该圆的半径r=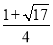 .
.
考点: 二次函数综合题.


科目:初中数学 来源:2013-2014学年江苏省江阴市九年级下学期期中考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中A(2,0),以A为圆心,1为半径作⊙A,若P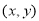 是⊙A上任意一点,则
是⊙A上任意一点,则 的最大值为( )
的最大值为( )
A.1 B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省昆山市九年级下学期教学质量调研(二模)数学试卷(解析版) 题型:解答题
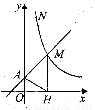
如图,直线y=x+1与y轴交于A点,与反比列函数y= (x>0)的图象交于点M,过M作MH⊥x,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x,且tan∠AHO=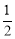 .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数y= (x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省昆山市九年级下学期教学质量调研(二模)数学试卷(解析版) 题型:选择题
把二次函数y=ax2+bx+c的图像向左平移4个单位或向右平移1个单位后都会经过原点,则二次函数图像的对称轴与x轴的交点是
A.(-2.5,0) B.(2.5,0) C.(-1.5,0) D.(1.5,0)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省昆山市九年级下学期教学质量调研(二模)数学试卷(解析版) 题型:选择题
下列计算中,正确的是
A.3a-2a=1 B.(x+3y)2=x2+9y2
C.(x5)2=x7 D.3--2=
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市锡山区九年级下学期期中考试(一模)数学试卷(解析版) 题型:解答题
中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
(1)若在三艘海监船组成的△OBC区域内没有探测盲点,则雷达的有效探测半径r至少为_______海里;
(2)某时刻海面上出现一艘菲律宾海警船A,在海监船C测得点A位于南偏东60°方向上,同时在海监船B测得A位于北偏东45°方向上,海警船A正以每小时20海里的速度向正西方向移动,我海监船B立刻向北偏东15°方向运动进行拦截,问我海监船B至少以多少速度才能在此方向上拦截到菲律宾海警船A?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com