
【题目】随着“一带一路”的不断建设与深化,我国不少知名企业都积极拓展海外市场,参与投资经营.某著名手机公司在某国经销某种型号的手机,受该国政府经济政策与国民购买力双重影响,手机价格不断下降.分公司在该国某城市的一家手机销售门店,今年5月份的手机售价比去年同期每台降价1000元,若卖出同样多的手机,去年销售额可达10万元,今年销售额只有8万元.
(1)今年5月份每台手机售价多少元?
(2)为增加收入,分公司决定拓展产品线,增加经销某种新型笔记本电脑.已知手机每台成本为3500元,笔记本电脑每台成本为3000元,分公司预计用不少于4.8万元的成本资金少量试生产这两种产品共15台,但因资金所限不能超过5万元,共有几种生产方案?
(3)如果笔记本电脑每台售价3800元,现为打开笔记本电脑的销路,公司决定每售出1台笔记本电脑,就返还顾客现金a元,要使(2)中各方案获利最大,a的值应为多少?最大利润多少?
【答案】(1)今年5月份每台手机售价4000元;(2)5种生产方案;(3)a的值应为300元,最大利润为7500元.
【解析】
(1)设今年5月份手机每台售价为m元,则去年同期每台售价为(m+1000)元,根据数量=总价÷单价结合今年5月份与去年同期的销售数量相同,即可得出关于m的分式方程,解之经检验后即可得出结论;
(2)设生产手机x台,则生产笔记本电脑(15-x)台,根据总价=单价×数量结合总价不少于4.8万元不能超过高于5万元,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,由该范围内整数的个数即可得出方案的种数;
(3)设总获利为w元,根据利润=销售收入-成本,即可得出w关于x的一次函数关系式,由w的值与x无关,即可得出a-300=0,解之即可求出a值.
(1)设今年5月份手机每台售价为m元,则去年同期每台售价为(m+1000)元,
根据题意得:![]() ,
,
解得:m=4000,
经检验,m=4000是原方程的根且符合题意.
答:今年5月份手机每台售价为4000元.
(2)设生产手机x台,则生产笔记本电脑(15-x)台,
根据题意得: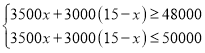 ,
,
解得:6≤x≤10,
∴x的正整数解为6、7、8、9、10.
答:共有5种生产方案.
(3)设总获利为w元,
根据题意得:w=(4000-3500)x+(3800-3000-a)(15-x)=(a-300)x+12000-15a.
∵w的值与x值无关,
∴a-300=0,即a=300.
当a=300时,最大利润为12000-15×300=7500元.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若每个房间定价增加40元,则这个宾馆这一天的利润为多少元?
(2)若宾馆某一天获利10640元,则房价定为多少元?
(3)房价定为多少时,宾馆的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A. 红红不是胜就是输,所以红红胜的概率为![]()
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为![]()
D. 娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
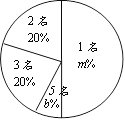
【题目】为了有效地落实国家精准扶贫政策,切实关爱贫困家庭学生.某校对全校各班贫困家庭学生的人数情况进行了调查.发现每个班级都有贫困家庭学生,经统计班上贫困家庭学生人数分别有1名、2名、3名、5名,共四种情况,并将其制成了如下两幅不完整的统计图:
(1)填空:a = ,b= ;
(2)求这所学校平均每班贫困学生人数;
(3)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表或画树状图的方法,求出被选中的两名学生来自同一班级的概率.
贫困学生人数 | 班级数 |
1名 | 5 |
2名 | 2 |
3名 | a |
5名 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,直线l⊥y轴于点C(C在y轴的正半轴上),与直线y=![]() 相交于点A,和双曲线y=
相交于点A,和双曲线y=![]() 交于点B,且AB=6,则点B的坐标是______.
交于点B,且AB=6,则点B的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
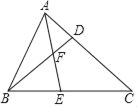
【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若![]() ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() ,边
,边![]() 落在
落在![]() 正半轴上,
正半轴上,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 分别作
分别作![]() ,
,![]() 交平行四边形各边如图.若反比例函数
交平行四边形各边如图.若反比例函数![]() 的图象经过点
的图象经过点![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为__.
的值为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com