Question

【题目】如图，平面直角坐标系中，平行四边形的顶点，边落在正半轴上，为线段上一点，过点分别作，交平行四边形各边如图．若反比例函数的图象经过点，四边形的面积为，则的值为__．

Answer 1

【答案】

【解析】

过C作CM⊥x轴于点M，由平行四边形DCOE的面积可求得OE，过D作DN⊥x轴于点N，由C点坐标则可求得ON的长，从而可求得D点坐标，代入反比例函数解析式可求得k的值

如图，过C作CM⊥x轴于点M，过D作DN⊥x轴于点N，则四边形CMND为矩形，

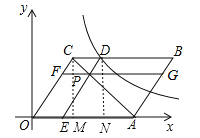
∵四边形OABC为平行四边形，

∴CD∥OE，且DE∥OC，

∴四边形DCOE为平行四边形，

∵C（2，5），

∴OM=2，CM=5，

由图可得，S△AOC＝S△ABC＝SABCO，

又∵S△FCP=S△DCP且S△AEP=S△AGP，

∴SOEPF=SBGPD，

∵四边形BCFG的面积为10，

∴SCDEO=SBCFG=10，

∴S四边形DCOE=OECM=10，即5OE=10，解得OE=2，

∴CD=MN=2，

∴ON=OM+MN=2+2=4，DN=CM=5，

∴D（4，5），

∵反比例函数y=图象过点D，

∴k=4×5=20.

故答案为：20.