
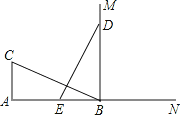
【题目】如图,CA⊥AB,垂足为点A,AB=12,AC=6,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过 秒时,△DEB与△BCA全等.
【答案】0,3,9,12.
【解析】
试题分析:此题要分两种情况:①当E在线段AB上时,②当E在BN上,再分别分成两种情况AC=BE,AC=BE进行计算即可.
试题解析:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=6,
∴BE=6,
∴AE=2-6=6,
∴点E的运动时间为6÷2=3(秒);
②当E在BN上,AC=BE时,
AC=12+6=18,
点E的运动时间为18÷2=9(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
AE=12+12=24,
点E的运动时间为24÷2=12(秒),


科目:初中数学 来源: 题型:
【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)计算两班的优秀率.
(2)计算两班比赛数据的方差.
(3)根据以上信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在一次函数y=kx+3中,函数值y随x的增大而增大,请你写出一个符合条件的k的值:_______.
(2)已知一个函数,当x>0时,函数值y随x的增大而减小,请你写出符合条件的一个函数表达式:_________.
(3)若一次函数y=kx+b的图象经过点(0,-2)和(-2,0),则y随x的增大而_______.
(4)若点(-1,y1),(2,y2)是直线y=2x+1上的两点,则y1___y2(填“>”“<”或“=”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC. 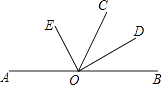
(1)求∠EOD的度数;
(2)若∠AOE=50°,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com