
����Ŀ��ijСѧ��չ4�ֿ�����ȤС�����ֱ�ΪA���滭��B�������ˣ�C�����裺D��������ÿ��ѧ����Ҫѡȡһ����ȤС�������С����ͬѧ��ѡȡ�Ļ��ʽ����������������飬���ݵ���ͳ�ƽ�������������µ�ͳ��ͼ��

��1�����ε���ѧ������ ���ˣ�a=�� ������������ͼ����������
��2�������У��ѧ��500�ˣ���ѡ�����ˡ����ѧ�������ж����ˣ�
��3��ѧУ��ÿ��ͬѧ��A��B��C��D���ֻ��ʽ�У������ȡ���ֿ�չ���������״ͼ���б����ķ�������ÿ���ȡ��������ʽǡ���ǡ��滭���͡������ˡ��ĸ��ʣ�
���𰸡���1����������2��50�ˣ�3��![]()
����������1������ͳ��ͼ��A������������ռ�İٷֱȿɵõ�����������������ݰٷֱ�֮��Ϊ1�ɵ�a��ֵ��Ȼ�����������ֱ��ȥA��C��D��������õ�B���������ٲ�ȫ����ͳ��ͼ��
��2������������������B�İٷֱȿɵã�
��3������״ͼչʾ����12�ֵȿ��ܵĽ���������ҳ�ij�����鵽�����ʽǡ�������滭���������������Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
(1)���ε����ѧ������Ϊ120��40%=300(��)��
a%=140%30%20%=10%��
��a=10��
B�������Ϊ300��10%=30��
��ȫͼ�����£�
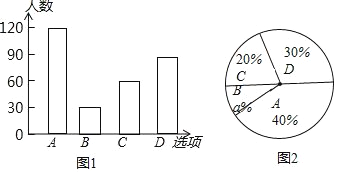
(2)500��10=50(��)��
��ѡ���������������ѧ��������50�ˣ�
(3)����״ͼΪ��

����12�ֵȿ��ܵĽ����������ij�����鵽�����ʽǡ�������滭���������������Ľ����Ϊ2��
����ij�����鵽�����ʽǡ�������滭���������������ĸ���![]()


 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A���D3��6����B���D9��һ3������ԭ��OΪλ�����ģ����Ʊ�Ϊ![]() ������ABO��С�����A�Ķ�Ӧ��A������������ ��
������ABO��С�����A�Ķ�Ӧ��A������������ ��

A�����D1��2��
B�����D9��18��
C�����D9��18����9���D18��
D�����D1��2����1���D2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�洬�����������У���![]() ���ú���
���ú���![]() λ�ڱ�ƫ��
λ�ڱ�ƫ��![]() �ķ���ǰ��
�ķ���ǰ��![]() ���ﵽ��
���ﵽ��![]() �㣬��ʱ����ú���
�㣬��ʱ����ú���![]() λ�ڱ�ƫ��
λ�ڱ�ƫ��![]() �ķ�����
�ķ�����![]() ������
������![]() �ľ���
�ľ���![]() ����________���
����________���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E����ABC�����ģ�AE���ӳ��߽���ABC�����Բ�ڵ�D.
��1��BD��DE�����Ϊʲô?
��2������BAC=90�㣬DE=4������ABC���Բ�İ뾶.
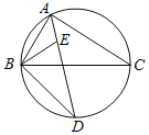
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A(2,1)������������ykx(����k0)�ͷ���������y![]() (����t0)��ͼ���ڵ�һ���Ľ��㣬��B������������ͼ�����һ�����㣬��C��x����һ�㣮
(����t0)��ͼ���ڵ�һ���Ľ��㣬��B������������ͼ�����һ�����㣬��C��x����һ�㣮
��1���������������Ľ���ʽ��ֱ��д����B�����ꣻ
��2����ABCΪ����������ʱ,��C�����꣮
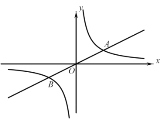
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A��60������D��BC�ߵ��е㣬DE��BC����ABC��ƽ����BF��DE����ABC��һ��P������PC��
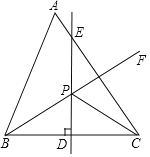
��1������ABP��32�������ACP�Ķ�����
��2������ACP��m������ABP��n������ֱ��д��m��n����Ĺ�ϵʽ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��y=kx2+��3k+2��x+1���������⸺ʵ��k����x��mʱ��y��x�������������m���������ֵΪ��������
A. 2 B. ��2 C. ��1 D. 0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=BC=2����ABC=120��������ABC���ŵ�B˳ʱ����ת��a��0�㣼a��90�����õ���A1BC��A1B��AC�ڵ�E��A1C1�ֱ�AC��BC��D��F���㣮
��1����ͼ1���۲첢���룬����ת�����У��߶�BE��BF��������������ϵ����֤����Ľ��ۣ�
��2����ͼ2����a=30��ʱ�����ж��ı���BC1DA����״����֤����
��3���ڣ�2���������£����߶�DE�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı��� ABCD����A=90�㣬AB=3m��BC=12m��CD=13m��DA=4m��
(1)��֤��BD��CB��
(2)���ı��� ABCD �������
(3)��ͼ 2���� A Ϊ����ԭ�㣬�� AB��AD����ֱ��Ϊ x�ᡢy�Ὠ��ֱ������ϵ��
��P��y���ϣ��� S��PBD=![]() S�ı���ABCD���� P�����꣮
S�ı���ABCD���� P�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com