
【题目】(1)﹣![]() ﹣
﹣![]() ﹣(﹣
﹣(﹣![]() )﹣
)﹣![]()
(2)9.872+(﹣![]() )+(﹣5.872)
)+(﹣5.872)
(3)(![]() ﹣
﹣![]()
![]() )÷(﹣
)÷(﹣![]() );
);
(4)![]()
![]()
(5)1.3×(﹣9.12)+(﹣7)×9.12
(6)﹣14﹣![]() ×[2﹣(﹣3)]2
×[2﹣(﹣3)]2
(7)[![]() ÷(﹣
÷(﹣![]() )+0.4×
)+0.4×![]() ]×(﹣1)5
]×(﹣1)5
(8)[1![]() ]2÷[(1﹣
]2÷[(1﹣![]() )×
)×![]() ]3.
]3.
【答案】(1)﹣![]() .(2)
.(2)![]() .(3)﹣
.(3)﹣![]() .(4)
.(4)![]() .(5)﹣75.696.(6)﹣
.(5)﹣75.696.(6)﹣![]() .(7)12.5.(8)﹣
.(7)12.5.(8)﹣![]() .
.
【解析】
试题分析:(1)最简公分母为12,通分化简即可.
(2)第一个数和第三个数先加减,再利用分数的通分法则计算.
(3)先去括号可以简便运计算.
(4)先计算中括号后计算除法.
(5)逆用加法分配律可以简便计算.
(6)先计算乘方,再计算括号,最后计算加减.
(7)先乘方后乘除最后计算加减.
(8)先计算括号后计算乘方再计算乘除.
解:(1)原式=﹣![]() ﹣
﹣![]() +
+![]() ﹣
﹣![]() =﹣
=﹣![]() =﹣
=﹣![]() .
.
(2)原式=4﹣![]() =
=![]() .
.
(3)原式=﹣![]() ×
×![]() +
+![]() ×
×![]() ﹣
﹣![]() ×
×![]() =﹣
=﹣![]() +
+![]() ﹣
﹣![]() =﹣
=﹣![]() .
.
(4)原式=![]() ÷[
÷[![]() +
+![]() ﹣
﹣![]() ]=
]=![]() ÷
÷![]() =
=![]() .
.
(5)原式=﹣9.12×(1.3+7)=﹣9.12×8.3=﹣75.696.
(6)原式=﹣1﹣![]() ×25=﹣
×25=﹣![]() .
.
(7)原式=[![]() ×(﹣4)+0.4×
×(﹣4)+0.4×![]() ]×(﹣1)=﹣(﹣15+2.5)=12.5.
]×(﹣1)=﹣(﹣15+2.5)=12.5.
(8)原式=[![]() ×
×![]() ]2÷[
]2÷[![]() ×(﹣
×(﹣![]() )]3=
)]3=![]() ÷(﹣
÷(﹣![]() )3=﹣
)3=﹣![]() ×27=﹣
×27=﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要对一块长60米,宽40米的矩形荒地ABCD进行绿化和硬化、设计方案如图所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形ABCD面积的![]() ,求P、Q两块绿地周围的硬化路面的宽.
,求P、Q两块绿地周围的硬化路面的宽.
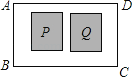
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD顶点C的坐标为(5,4),顶点A在x轴的正半轴上,反比例函数y=![]() 的图象经过AC与BD的交点E,与边BC交于点F.
的图象经过AC与BD的交点E,与边BC交于点F.
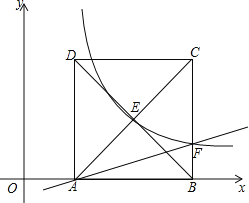
(1)求反比例函数的解析式;
(2)求直线AF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
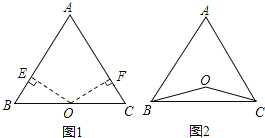
(1)如图1,若点O在边BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com