
【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?

【答案】答案见解析
【解析】试题分析:根据面积相等的法则进行计算.
试题解析:方法1:∵由图(a)可知S正方形ACFD=S四边形ABFE ,
∴S正方形ACFD=S⊿BAE+S⊿BFE
又∵正方形ACFD的边长为b, SRt△BAE=![]() ,SRt△BFE=
,SRt△BFE=![]()
∴b2 =![]() +
+![]()
即2b2 =c2 +(b+a)(b-a)
整理得: a2+b2=c2
方法2:如图(b)中,Rt△BEA和Rt△ACD全等, 设CD=a,AC=b,AD=c(b>a),
则AE=a,BE=b,AB=c,EC=b-a
由图(b),S四边形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD
又∵SRt△BAE =![]() , SRt△ACD =
, SRt△ACD =![]() ,SRt△BEC=
,SRt△BEC=![]() ,
,
SRt△BAD=![]() ,S△BCD=
,S△BCD=![]() ,
,
∴![]() +
+![]() +
+![]() =
=![]() +
+![]()
即2ab+b(b-a)= c2 +a(b-a)
整理得: a2+b2=c2


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】 小明同学5次数学单元测试的平均成绩是90分,中位数是91分,众数是94分,则两次最低成绩之和是( )
A. 165分 B. 168分 C. 170分 D. 171分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次水灾中,大约有2.5×105个人无家可归,假如一顶帐篷占地100米2,可以放置40个床位,为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约要占多少地方?估计你的学校的操场可安置多少人?要安置这些人,大约需要多少个这样的操场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)

(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
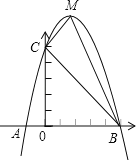
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
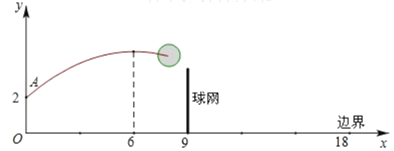
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2![]() 的A处发出,把球看成点,其运行的高度
的A处发出,把球看成点,其运行的高度![]() 与运行的水平距离
与运行的水平距离![]() 满足关系式
满足关系式![]() .已知球网与O点的水平距离为9
.已知球网与O点的水平距离为9![]() ,高度为2.43
,高度为2.43![]() ,球场的边界距O点的水平距离为18
,球场的边界距O点的水平距离为18![]() .
.
(1)当![]() =2.6时,求
=2.6时,求![]() 与
与![]() 的关系式(不要求写出自变量
的关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(2)当![]() =2.6时,球能否越过球网?球会不会出界?请说明理由;
=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求二次函数中![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)﹣![]() ﹣
﹣![]() ﹣(﹣
﹣(﹣![]() )﹣
)﹣![]()
(2)9.872+(﹣![]() )+(﹣5.872)
)+(﹣5.872)
(3)(![]() ﹣
﹣![]()
![]() )÷(﹣
)÷(﹣![]() );
);
(4)![]()
![]()
(5)1.3×(﹣9.12)+(﹣7)×9.12
(6)﹣14﹣![]() ×[2﹣(﹣3)]2
×[2﹣(﹣3)]2
(7)[![]() ÷(﹣
÷(﹣![]() )+0.4×
)+0.4×![]() ]×(﹣1)5
]×(﹣1)5
(8)[1![]() ]2÷[(1﹣
]2÷[(1﹣![]() )×
)×![]() ]3.
]3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com