
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
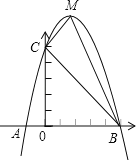
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.
【答案】(1)y=﹣x2+4x+5;(2)15.
【解析】
试题分析:(1)将已知的三点坐标代入抛物线中,即可求得抛物线的解析式.
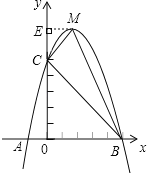
(2)可根据抛物线的解析式先求出M和B的坐标,由于三角形MCB的面积无法直接求出,可将其化为其他图形面积的和差来解.过M作ME⊥y轴,三角形MCB的面积可通过梯形MEOB的面积减去三角形MCE的面积减去三角形OBC的面积求得.
解:
(1)依题意: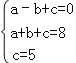 ,
,
解得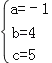
∴抛物线的解析式为y=﹣x2+4x+5
(2)令y=0,得(x﹣5)(x+1)=0,x1=5,x2=﹣1,
∴B(5,0).
由y=﹣x2+4x+5=﹣(x﹣2)2+9,得M(2,9)
作ME⊥y轴于点E,
可得S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC=![]() (2+5)×9﹣
(2+5)×9﹣![]() ×4×2﹣
×4×2﹣![]() ×5×5=15.
×5×5=15.


科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
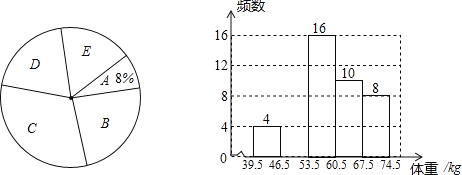
解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
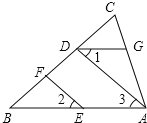
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①、②,解答下面各题:
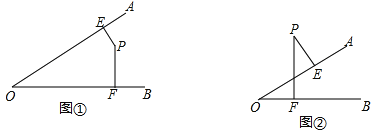
(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数。
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不成立的是( )
A.弦的垂直平分线必过圆心
B.弧的中点与圆心的连线垂直平分这条弧所对的弦
C.垂直于弦的直线经过圆心,且平分这条弦所对的弧
D.垂直于弦的直径平分这条弦
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
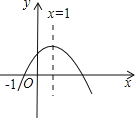
A.a>0
B.当﹣1<x<3时,y>0
C.c<0
D.当x≥1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=4,BC=3,以点D为圆心作圆,使A、B、C三点中至少有一点在圆内且至少一点在圆外,⊙O的的半径r的取值范围是_________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com