
【题目】已知:如图①、②,解答下面各题:
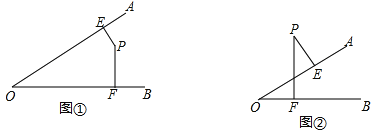
(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数。
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)
【答案】(1)125°;(2)∠P=∠O;(3)相等或互补;(4)相等或互补.
【解析】试题分析:(1)利用四边形的内角和定理即可求解;
(2)利用垂直的定义和三角形的内角和定理求解;
(3)根据(1)和(2)的结果即可求解;
(4)本题应分两种情况讨论,如图,∠1,∠2,∠3的两边互相平行,由图形可以看出∠1和∠2是邻补角,它们和∠3的关系容易知道一个相等,一个互补.
试题解析:(1)如图①,

∵PE⊥OA,PF⊥OB,
∴∠PEO=∠OFP=90°,
∴∠EPF=360°-90°-90°-55°=125°;
(2)如图②,
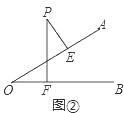
∵PE⊥OA,PF⊥OB,
∴∠PEO=∠OFP=90°,
又∵∠OGF=∠PGE,
∴∠P=∠O;
(3)如果一个角的两边分别垂直于另一个角的两边,则这两个角相等或互补;
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角相等或互补.
如图③,

∠1,∠2,∠3的两边互相平行,
∴∠3=∠4,∠4=∠1,∠4+∠2=180°;
∴∠3=∠1,∠3+∠2=180°.
∴这两个角相等或互补.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.
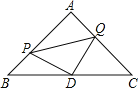
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】82m×4n÷2m﹣n
(2)6m362m÷63m﹣2
(3)(a4a3÷a2)3
(4)(﹣10)2+(﹣10)0+10﹣2×(﹣102)
(5)(![]() x6y5+
x6y5+![]() x5y4﹣
x5y4﹣![]() x4y3)÷
x4y3)÷![]() x3y3
x3y3
(6)![]() x﹣(2x﹣
x﹣(2x﹣![]() y2)+(
y2)+(![]() x﹣
x﹣![]() y2)
y2)
(7)2﹣[x﹣![]() (x﹣1)]﹣
(x﹣1)]﹣![]() (x﹣1)
(x﹣1)
(8)5xy2﹣{2x2y﹣[3xy2﹣(xy2﹣2x2y)]÷(﹣![]() xy)}.
xy)}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次水灾中,大约有2.5×105个人无家可归,假如一顶帐篷占地100米2,可以放置40个床位,为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约要占多少地方?估计你的学校的操场可安置多少人?要安置这些人,大约需要多少个这样的操场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽取6名同学参加体能测试,成绩如下:85,90,75,75,80,80.下列表述正确的是( )
A.众数是80 B.中位数是75
C.平均数是80 D.极差是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)

(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
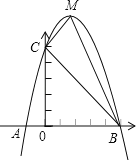
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
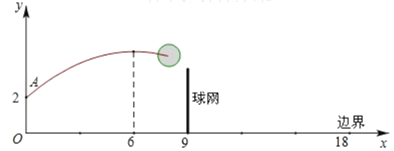
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2![]() 的A处发出,把球看成点,其运行的高度
的A处发出,把球看成点,其运行的高度![]() 与运行的水平距离
与运行的水平距离![]() 满足关系式
满足关系式![]() .已知球网与O点的水平距离为9
.已知球网与O点的水平距离为9![]() ,高度为2.43
,高度为2.43![]() ,球场的边界距O点的水平距离为18
,球场的边界距O点的水平距离为18![]() .
.
(1)当![]() =2.6时,求
=2.6时,求![]() 与
与![]() 的关系式(不要求写出自变量
的关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(2)当![]() =2.6时,球能否越过球网?球会不会出界?请说明理由;
=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求二次函数中![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
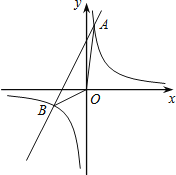
【题目】如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=![]() 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com