Question

【题目】如图，A（1，0）、B（7，0），⊙A、⊙B的半径分别为1和2，将⊙A沿x轴向右平移3个单位，则此时该圆与⊙B的位置关系是（ ）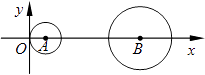
A.外切
B.相交
C.内含
D.外离

Answer 1

【答案】A
【解析】解：∵A（1，0）、B（7，0），⊙A、⊙B的半径分别为1和2， ∴⊙A、⊙B的圆心距为6，
∴⊙A沿x轴向右平移3个单位后，⊙A、⊙B的圆心距为3，
∴根据圆心距与半径之间的数量关系可知两圆的位置关系是外切．
故选A．
【考点精析】根据题目的已知条件，利用圆与圆的位置关系的相关知识可以得到问题的答案，需要掌握两圆之间有五种位置关系：无公共点的，一圆在另一圆之外叫外离，在之内叫内含；有唯一公共点的，一圆在另一圆之外叫外切，在之内叫内切；有两个公共点的叫相交．两圆圆心之间的距离叫做圆心距．两圆的半径分别为R和r，且R≥r，圆心距为P：外离P＞R+r；外切P=R+r；相交R-r＜P＜R+r；内切P=R-r；内含P＜R-r．