
【题目】如图,△ABC和△ECD都是等边三角形,B、C、D三点在一条直线上,AD与BE相交于点O,AD与CE相交于点F,AC与BE相交于点G.
(1)△BCE与△ACD全等吗?请说明理由.
(2)求∠BOD度数.
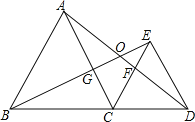
【答案】(1)△BCE≌△ACD.证明见解析;(2)120°.
【解析】
(1)通过观察图形,根据等边三角形的性质就可以证明△BCE≌△ACD;
(2)由(1)△BCE≌△ACD可以得出∠ADC=∠BEC,而有∠AOB=∠EBC+∠ADB,就有∠AOB=∠EBC+∠BEC=∠DCE=60°,从而可以求出∠BOD的值.
(1)△BCE≌△ACD.
理由:∵△ABC和△ECD都是等边三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=∠BAC=60°,
∴∠BCA+∠ACE=∠ECD+∠ACE,
∵∠BCE=∠ACD.
在△BCE和△ACD中,
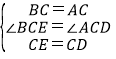 ,
,
∴△BCE≌△ACD(SAS);
(2)∵△BCE≌△ACD,
∴∠ADC=∠BEC.
∵∠AOB=∠EBC+∠ADC,
∴∠AOB=∠EBC+∠BEC=∠DCE=60°.
∵∠AOB+∠BOD=180°,
∴∠BOD=120°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图.已知A、B两点的坐标分别为A(0,![]() ),B(2,0).直线AB与反比例函数
),B(2,0).直线AB与反比例函数![]() 的图象交于点C和点D(
的图象交于点C和点D(![]() 1,a).
1,a).
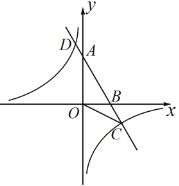
(1)求直线AB和反比例函数的解析式.
(2)求∠ACO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
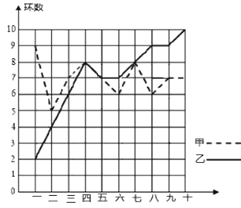
(1)请将下表补充完整:
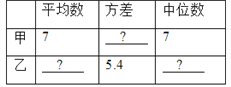
(2)请从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弦AB,CD是⊙O的两条平行弦,⊙O的半径为5,AB=8,CD=6,则AB,CD之间的距离为( )
A. 7 B. 1 C. 4或3 D. 7或1
查看答案和解析>>
科目:初中数学 来源: 题型:
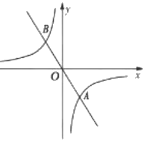
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= -2x和反比例函数![]() 的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线
的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线![]() 交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小明的做法如下:
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n,与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P,连结AP,BP.
所以∠APB=∠ACB.
老师说:“小明的作法正确.”
请回答:
(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
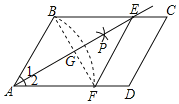
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com