
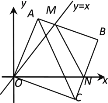
【题目】在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点。现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为________
【答案】4.
【解析】
利用全等把△MBN的各边整理到成与正方形的边长有关的式子即可.
解:如图所示:延长BA交y轴于E点,
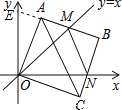
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN,
在△OAE和△OCN中,
∠EOA=∠CON,OA=OC,∠OAE=∠OCN,
,
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中,
OE=OC,∠EOM=∠COM,OM=OM,
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
∴△MBN的周长=MN+BN+BM=AM+CN+BN+BM=AB+BC=6.
“点睛”此题主要考查了旋转的性质以及全等三角形的判定与性质等知识,注意求一些线段的长度或角的度数,总要整理到已知线段的长度上或已知角的度数上进而得出是解题关键.


科目:初中数学 来源: 题型:
【题目】阅读材料并完成任务.

莱昂哈德·欧拉是18世纪数学界最杰出的人物之一,瑞士著名的数学家、物理学家,他不但为数学界作出贡献,更把整个数学推至物理的领域;同时,也是数学史上研究成果最多的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学等的课本,《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作.因此,被称为历史上最伟大的两位数学家之一(另一位是卡尔·弗里德里克·高斯).在数学成就上,欧拉最先把关于![]() 的多项式用记号
的多项式用记号![]() 的形式来表示(
的形式来表示(![]() 可用其他字母代替,但不同的字母表示不同的多项式),例如
可用其他字母代替,但不同的字母表示不同的多项式),例如![]() ,当
,当![]() 时,多项式的值用
时,多项式的值用![]() 来表示,即
来表示,即![]() ;当
;当![]() 时,多项式的值用
时,多项式的值用![]() 来表示,记为
来表示,记为![]() .
.
任务:
已知![]() ;
;![]() .
.
请你根据材料中代入求值的方法解决下列问题:
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
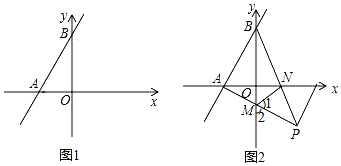
【题目】如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于点![]() 点
点![]() 且a、b满足
且a、b满足![]() .
.
![]() ______;
______;![]() ______.
______.
![]() 点P在直线AB的右侧,且
点P在直线AB的右侧,且![]() ,
,
![]() 若点P在x轴上,则点P的坐标为______;
若点P在x轴上,则点P的坐标为______;
![]() 若
若![]() 为直角三角形,求点P的坐标;
为直角三角形,求点P的坐标;
![]() 如图2,在
如图2,在![]() 的条件下,
的条件下,![]() 且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接
且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接![]() 求证:
求证:![]() 提示:过点P作
提示:过点P作![]() 交x轴于
交x轴于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.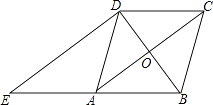
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.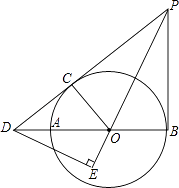
(1)求证:PB是⊙O的切线;
(2)若PB=9,DB=12,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]()
(1)请直接写出方程![]() 的所有正整数解
的所有正整数解
(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为 a,宽为 b 的长方形.现将相等的长方形若干,拼接组成如下图 形.
(1)将图①中所得的四块长为 a,宽为 b 的小长方形拼成一个正方形(如图②).请利用 图②中阴影部分面积的不同表示方法,直接写出代数式(a+b)2、(a﹣b)2、ab 之间的等量关系是 ;
(2)根据(2)题中的等量关系,解决如下问题:已知 m+n=6,mn=5,则 m﹣n= ;
(3)将图①中的长方形和图③中的两个边长分别为 a、b 的正方形若干个,拼成如图④的长方形,则图④中的长方形的面积可以用两种不同的方法表示,则关系式 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣4![]() x+12+m=0.
x+12+m=0.
(1)若方程的一个根是![]() ,求m的值及方程的另一根;
,求m的值及方程的另一根;
(2)若方程的两根恰为等腰三角形的两腰,而这个三角形的底边为m,求m的值及这个等腰三角形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com