
【题目】图①是一个长为 a,宽为 b 的长方形.现将相等的长方形若干,拼接组成如下图 形.
(1)将图①中所得的四块长为 a,宽为 b 的小长方形拼成一个正方形(如图②).请利用 图②中阴影部分面积的不同表示方法,直接写出代数式(a+b)2、(a﹣b)2、ab 之间的等量关系是 ;
(2)根据(2)题中的等量关系,解决如下问题:已知 m+n=6,mn=5,则 m﹣n= ;
(3)将图①中的长方形和图③中的两个边长分别为 a、b 的正方形若干个,拼成如图④的长方形,则图④中的长方形的面积可以用两种不同的方法表示,则关系式 .

【答案】(1)(a﹣b)2=(a+b)2﹣4ab;(2)±4;(3)(2a+b)(a+b)=2a2+3ab+b2.
【解析】
(1)利用大正方形的面积减4个小长方形的面积等于小正方形的面积列式即可;
(2)利用公式(m﹣n)2=(m+n)2﹣4mn求解即可;
(3)根据大长方形面积等于长乘以宽或2个边长为a的正方形、1个边长为b的正方形加上3个长为a、宽为b的小长方形面积和列式可得.
解:(1)(a﹣b)2=(a+b)2﹣4ab.
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(2)∵m+n=6,mn=5,
∴(m﹣n)2=(m+n)2﹣4mn=36﹣20=16,
∴m﹣n=±4
故答案为:±4;
(3)根据大长方形面积等于长乘以宽有:(2a+b)(a+b),
或2个边长为a的正方形、1个边长为b的正方形加上3个长为a、宽为b的小长方形面积和有:2a2+3ab+b2,
故可得:(2a+b)(a+b)=2a2+3ab+b2.
故答案为:(2a+b)(a+b)=2a2+3ab+b2.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】一般地,![]() 个相同的因数
个相同的因数![]() 相乘
相乘![]() ,记为
,记为![]() , 如
, 如![]() ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为![]() (即
(即![]() ) .一般地,若
) .一般地,若![]() 且
且![]() , 则
, 则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数, 记为
的对数, 记为![]() (即
(即![]() ) .如
) .如![]() , 则4叫做以3为底81的对数, 记为
, 则4叫做以3为底81的对数, 记为![]() (即
(即![]() ) .
) .
(1)计算下列各对数的值:![]() ;
;![]() ;
;![]() .
.
(2)观察(1)中三数4、16、64之间满足怎样的关系式,![]() 之间又满足怎样的关系式;
之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
(4) 根据幂的运算法则:![]() 以及对数的含义说明上述结论.
以及对数的含义说明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点。现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为________
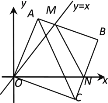
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,且与y轴相交于点C,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为直角三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有______________
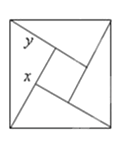
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名选手在同等条件下进行射击对抗赛,他们各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数 | 众数 | 中位数 | 方差 | 10环次数 | |
甲 | 8 | ||||
乙 |

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
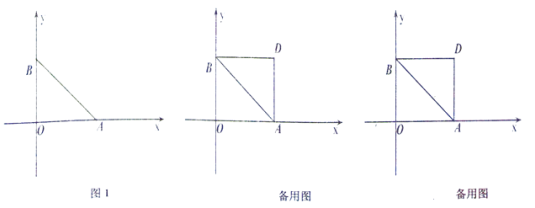
【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(a,0)、B(b,O)分别在x轴正半轴和y轴正半轴上,且![]() ,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.
,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.
(1)求点A、B的坐标;
(2)连接PB,设三角形ABP的面积为s,点P的运动时间为t,请用含t的式子表示s,并直接写出t的取值范围;
(3)在(2)的条件下,将线段OB沿x轴正方向平移,使点O与点A重合,点B的对应点为点D,连接BD,将线段PB沿x轴正方向平移,使点B与点D重合,点P的对应点为点Q,取DQ的中点H,是否存在t的值,使三角形ABP的面积等于三角形ADH的面积?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com