
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,且与y轴相交于点C,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为直角三角形,请直接写出所有符合条件的点M的坐标.
【答案】
(1)解:∵抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3
(2)解:如图1,
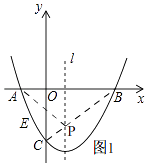
∵点A,B关于直线l对称,
∴连接BC交直线l于点P,
由(1)知,抛物线的解析式为y=x2﹣2x﹣3,
∴直线l:x=1,C(0,﹣3),
∵B(3,0),
∴直线BC的解析式为y=x﹣3,
当x=1时,y=﹣2,
∴P(1,﹣2)
(3)解:设点M(1,m),
∵A(﹣1,0),C(0,﹣3),
∴AC2=10,AM2=m2+4,CM2=(m+3)2+1=m2+6m+10,
∵△MAC为直角三角形,
∴当∠ACM=90°时,∴AC2+CM2=AM2,
∴10+m2+6m+10=m2+4,
∴m=﹣ ![]() ,
,
∴M(1,﹣ ![]() )
)
当∠CAM=90°时,∴AC2+AM2=CM2,
∴10+m2+4=m2+6m+10,
∴m= ![]() ,
,
∴M(1, ![]() )
)
当∠AMC=90°时,AM2+CM2=AC2,
∴m2+4+m2+6m+10=10,
∴m=﹣1或m=﹣2,
∴M(1,﹣1)或(1,﹣2),
即:满足条件的点M的坐标为(1,﹣ ![]() )或(1,
)或(1, ![]() )或(1,﹣1)或(1,﹣2)
)或(1,﹣1)或(1,﹣2)
【解析】(1)方法一、将A、B两点坐标代入函数解析式即可求。方法二、A、B两点是抛物线与x轴的交点坐标,a=1可设抛物线解析式为y=(x+1)(x-3).
(2)由题意可知点A,B关于直线l对称,连接BC交直线l于点P,求出直线BC的函数解析式,即可求出点P的坐标。
(3)由于点M也是直线l上的动点,△MAC为直角三角形,因此设点M(1,m),根据A、C两点坐标,分别求出AC2、AM2、CM2。再分三种情况:当∠ACM=90°时,∴AC2+CM2=AM2,当∠CAM=90°时,∴AC2+AM2=CM2,当∠AMC=90°时,AM2+CM2=AC2,分别建立方程,求出m的值,即可求得点m的坐标。
【考点精析】本题主要考查了确定一次函数的表达式和轴对称-最短路线问题的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能正确解答此题.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣2a3b(﹣4a2b)÷6a4b2
(2)![]()
(3)![]()
(4)(2a﹣1)(a﹣4)﹣(a+3)(a﹣4)
(5)(x﹣3y+4)(x+3y﹣4)
(6)(a+2b)(a﹣2b)(a2﹣4b2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年两会提出:随着城镇化水平的提高,为了房地产去库存,国家鼓励农民进城买房,可享受政府担保免收利息的惠民政策,小王家购买了一套学区房,首付15万元后,剩余部分贷款,贷款金额按月分期还款,每月还款数相同,计划每月还款y万元,x个月还清贷款,已知y是x的反比例函数,其图象如图所示.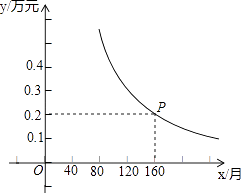
(1)求y与x的函数解析式(关系式),并求小王家购买的学区房的总价是多少万元?
(2)若计划80个月还清贷款,则每月应还款多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为 a,宽为 b 的长方形.现将相等的长方形若干,拼接组成如下图 形.
(1)将图①中所得的四块长为 a,宽为 b 的小长方形拼成一个正方形(如图②).请利用 图②中阴影部分面积的不同表示方法,直接写出代数式(a+b)2、(a﹣b)2、ab 之间的等量关系是 ;
(2)根据(2)题中的等量关系,解决如下问题:已知 m+n=6,mn=5,则 m﹣n= ;
(3)将图①中的长方形和图③中的两个边长分别为 a、b 的正方形若干个,拼成如图④的长方形,则图④中的长方形的面积可以用两种不同的方法表示,则关系式 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )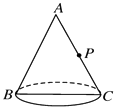
A.3 ![]() cm
cm
B.3 ![]() cm
cm
C.9cm
D.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合与实践课上老师将直尺摆放在三角板上,使直尺与三角板的边分别交于点P、M、N、Q,
(1)如图①所示.当∠CNG=42°,求∠HMC 的度数.(写出证明过程)
(2)将直尺向下平移至图 2 位置,使直尺的边缘通过点 C,交 AB 于点 P,直尺另一侧与三角形交于 N、Q 两点。请直接写出∠PQF、∠A、∠ACE 之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1= ![]() x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣
x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣ ![]() ,0).
,0).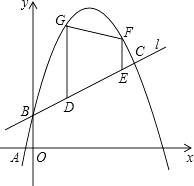
(1)求二次函数的最大值;
(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程 ![]() =0的根,求a的值;
=0的根,求a的值;
(3)若点F、G在图象C′上,长度为 ![]() 的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
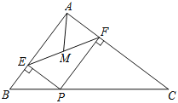
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com