
【题目】如图,已知一次函数y1= ![]() x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣
x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣ ![]() ,0).
,0).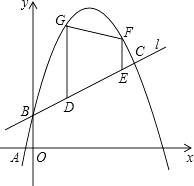
(1)求二次函数的最大值;
(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程 ![]() =0的根,求a的值;
=0的根,求a的值;
(3)若点F、G在图象C′上,长度为 ![]() 的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
【答案】
(1)解:∵二次函数y2=﹣x2+mx+b经过点B(0,1)与A(2﹣ ![]() ,0),
,0),
∴ ![]() ,
,
解得 ![]()
∴l:y1= ![]() x+1;
x+1;
C′:y2=﹣x2+4x+1.
∵y2=﹣x2+4x+1=﹣(x﹣2)2+5,
∴ymax=5
(2)解:联立y1与y2得: ![]() x+1=﹣x2+4x+1,解得x=0或x=
x+1=﹣x2+4x+1,解得x=0或x= ![]() ,
,
当x= ![]() 时,y1=
时,y1= ![]() ×
× ![]() +1=
+1= ![]() ,
,
∴C( ![]() ,
, ![]() ).
).
使y2>y1成立的x的取值范围为0<x< ![]() ,
,
∴s=1+2+3=6.
代入方程得 ![]()
解得a= ![]() ;
;
经检验a= ![]() 是分式方程的解
是分式方程的解
(3)解:∵点D、E在直线l:y1= ![]() x+1上,
x+1上,
∴设D(p, ![]() p+1),E(q,
p+1),E(q, ![]() q+1),其中q>p>0.
q+1),其中q>p>0.
如答图1,过点E作EH⊥DG于点H,则EH=q﹣p,DH= ![]() (q﹣p).
(q﹣p).

在Rt△DEH中,由勾股定理得:EH2+DH2=DE2,即(q﹣p)2+[ ![]() (q﹣p)]2=(
(q﹣p)]2=( ![]() )2,
)2,
解得q﹣p=2,即q=p+2.
∴EH=2,E(p+2, ![]() p+2).
p+2).
当x=p时,y2=﹣p2+4p+1,
∴G(p,﹣p2+4p+1),
∴DG=(﹣p2+4p+1)﹣( ![]() p+1)=﹣p2+
p+1)=﹣p2+ ![]() p;
p;
当x=p+2时,y2=﹣(p+2)2+4(p+2)+1=﹣p2+5,
∴F(p+2,﹣p2+5),
∴EF=(﹣p2+5)﹣( ![]() p+2)=﹣p2﹣
p+2)=﹣p2﹣ ![]() p+3.
p+3.
S四边形DEFG= ![]() (DG+EF)EH=
(DG+EF)EH= ![]() [(﹣p2+
[(﹣p2+ ![]() p)+(﹣p2﹣
p)+(﹣p2﹣ ![]() p+3)]×2=﹣2p2+3p+3
p+3)]×2=﹣2p2+3p+3
∴当p= ![]() 时,四边形DEFG的面积取得最大值,
时,四边形DEFG的面积取得最大值,
∴D( ![]() ,
, ![]() )、E(
)、E( ![]() ,
, ![]() ).
).
如答图2所示,过点D关于x轴的对称点D′,则D′( ![]() ,﹣
,﹣ ![]() );
);
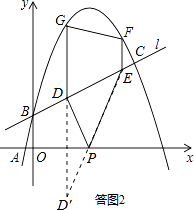
连接D′E,交x轴于点P,PD+PE=PD′+PE=D′E,
由两点之间线段最短可知,此时PD+PE最小.
设直线D′E的解析式为:y=kx+b,
则有 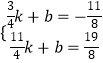 ,
,
解得 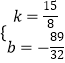
∴直线D′E的解析式为:y= ![]() x﹣
x﹣ ![]() .
.
令y=0,得x= ![]() ,
,
∴P( ![]() ,0).
,0).
【解析】(1)用待定系数法将点B、点A代入一次函数解析式和二次函数解析式,就可以求出两函数的解析式,再求出二次函数的顶点坐标,即可求出函数的最大值。
(2)先求出抛物线与直线BC的两交点坐标,观察图像,写出使y2>y1成立的x的取值范围,求出所有整数的和s的值,再将x=s代入方程,既可求出a的值。注意:此方程式分式方程必须检验。
(3)抓住已知条件中的长度为 5 的线段DE在线段BC上移动,EF与DG始终平行于y轴,因此添加辅助线,过点E作EH⊥DG于点H,D、E两点再直线BC上,设出这两点的坐标,根据勾股定理,得出EH=2,E(p+2,![]() p+2),再将当x=p时,当x=p+2时,分别代入二次函数解析式,求出对应的函数值,即可表示出点F、点G的坐标,再求出DG、EF的长,根据梯形的面积求出s与t的函数关系式,求出顶点坐标,即可求得p的值,并求出点D、E的坐标,要在x轴上求点P,使PD+PE最小,因此过点D作关于x轴的对称点D′,,求出直线D′E的解析式,即可求出点P的坐标
p+2),再将当x=p时,当x=p+2时,分别代入二次函数解析式,求出对应的函数值,即可表示出点F、点G的坐标,再求出DG、EF的长,根据梯形的面积求出s与t的函数关系式,求出顶点坐标,即可求得p的值,并求出点D、E的坐标,要在x轴上求点P,使PD+PE最小,因此过点D作关于x轴的对称点D′,,求出直线D′E的解析式,即可求出点P的坐标
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对二次函数的最值的理解,了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;② BG=GC;③ AG∥CF;④∠GAE=45°.
则正确结论的个数有( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,且与y轴相交于点C,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为直角三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名选手在同等条件下进行射击对抗赛,他们各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数 | 众数 | 中位数 | 方差 | 10环次数 | |
甲 | 8 | ||||
乙 |

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线__________的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段__________最短,理由:______.
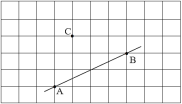
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,共有“一白三黑”四个围棋子,其除颜色外无其他区别.
(1)随机地从盒子中取出1子,则提出的是白子的概率是多少?
(2)随机地从盒子中取出1子,不放回再取出第二子,请用画树状或列表的方式表示出所有可能的结果,并求出恰好取出“一黑一白”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A,B两点,抛物线y=﹣x2+bx+c过A,B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.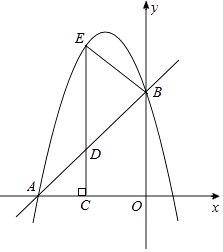
(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com