
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.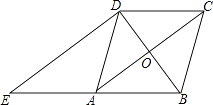
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∴AE∥CD,∠AOB=90°,
∵DE⊥BD,即∠EDB=90°,
∴∠AOB=∠EDB,
∴DE∥AC,
∴四边形ACDE是平行四边形
(2)解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AD=CD=5,
∵四边形ACDE是平行四边形,
∴AE=CD=5,DE=AC=8,
∴△ADE的周长为AD+AE+DE=5+5+8=18
【解析】(1)菱形的对角线互相垂直,对边平行得出AB∥CD,AC⊥BD,再根据已知DE⊥BD,从而证得DE∥AC,即可得出结论。
(2)要求△ADE的周长,根据已知就需求AD的长,根据菱形的性质,对角线互相垂直平分,在Rt△AOD中运用勾股定理求出AD的长,即可求出△ADE的周长。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲,乙两人以相同路线前往距离单位10![]() 的培训中心参加学习.图中
的培训中心参加学习.图中![]() 分别表示甲,乙两人前往目的地所走的路程s
分别表示甲,乙两人前往目的地所走的路程s![]() 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8![]() 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
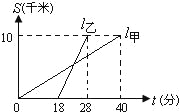
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,![]() 个相同的因数
个相同的因数![]() 相乘
相乘![]() ,记为
,记为![]() , 如
, 如![]() ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为![]() (即
(即![]() ) .一般地,若
) .一般地,若![]() 且
且![]() , 则
, 则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数, 记为
的对数, 记为![]() (即
(即![]() ) .如
) .如![]() , 则4叫做以3为底81的对数, 记为
, 则4叫做以3为底81的对数, 记为![]() (即
(即![]() ) .
) .
(1)计算下列各对数的值:![]() ;
;![]() ;
;![]() .
.
(2)观察(1)中三数4、16、64之间满足怎样的关系式,![]() 之间又满足怎样的关系式;
之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
(4) 根据幂的运算法则:![]() 以及对数的含义说明上述结论.
以及对数的含义说明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 、
、![]() 在坐标轴上,
在坐标轴上, ![]() 是
是![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的,点
得到的,点![]() 在
在![]() 轴上,直线
轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,线段
,线段![]() ,
,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,平面内是否存在点
轴上,平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请直接写出点
为顶点的四边形是矩形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=α.∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠A2019BC与∠A2019CD的平分线相交于点A2020,得∠A2020,则∠A2020=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;② BG=GC;③ AG∥CF;④∠GAE=45°.
则正确结论的个数有( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
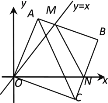
【题目】在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点。现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名选手在同等条件下进行射击对抗赛,他们各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数 | 众数 | 中位数 | 方差 | 10环次数 | |
甲 | 8 | ||||
乙 |

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com