
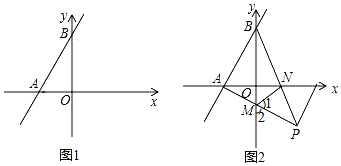
【题目】如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于点![]() 点
点![]() 且a、b满足
且a、b满足![]() .
.
![]() ______;
______;![]() ______.
______.
![]() 点P在直线AB的右侧,且
点P在直线AB的右侧,且![]() ,
,
![]() 若点P在x轴上,则点P的坐标为______;
若点P在x轴上,则点P的坐标为______;
![]() 若
若![]() 为直角三角形,求点P的坐标;
为直角三角形,求点P的坐标;
![]() 如图2,在
如图2,在![]() 的条件下,
的条件下,![]() 且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接
且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接![]() 求证:
求证:![]() 提示:过点P作
提示:过点P作![]() 交x轴于
交x轴于![]()
【答案】(1)![]() ,4;(2)
,4;(2)![]() ;
;![]() 或
或![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)![]() ,根据非负数的性质即可求解;
,根据非负数的性质即可求解;
(2)①点P在x轴上,则OP=OB=4,即可求解;②分∠BAP=90°、∠ABP=90°两种情况,求解即可;
![]() 通过证明△MEP≌△HFP(AAS)得:∠2=∠FHP,证明△MNP≌△HNP(SAS),∠1=∠NHP,即可求解.
通过证明△MEP≌△HFP(AAS)得:∠2=∠FHP,证明△MNP≌△HNP(SAS),∠1=∠NHP,即可求解.
解:![]() ,
,
即:![]() ,
,![]() ,
,
故答案是![]() ,4;
,4;
![]() 点P在x轴上,则
点P在x轴上,则![]() ,
,
故:答案是![]() ;
;
![]() 当
当![]() 时,
时,
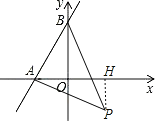
![]() ,
,![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
故点P的坐标为![]() ;
;
当![]() 时,
时,
同理可得:点P的坐标为![]() ,
,
故点P的坐标为![]() 或
或![]() ;
;
![]() 过点P作
过点P作![]() 交x轴于H,过点P分别作x、y轴的垂线,交于点F、E,
交x轴于H,过点P分别作x、y轴的垂线,交于点F、E,
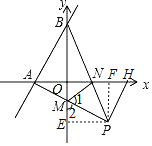
由![]() 知,
知,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.
故答案为:(1)-2, 4;(2)①(4, 0);②(2,-2)或(4,2);(3)见解析.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】若三角形的一边和该边上的高相等的三角形称为“和谐三角形”,如图,已知抛物线y=ax2经过A(﹣1,1),P是y轴正半轴上的动点,射线AP与抛物线交于另一点B,当△AOP是“和谐三角形”时,点B的坐标为 . 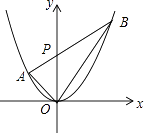
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,![]() 个相同的因数
个相同的因数![]() 相乘
相乘![]() ,记为
,记为![]() , 如
, 如![]() ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为![]() (即
(即![]() ) .一般地,若
) .一般地,若![]() 且
且![]() , 则
, 则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数, 记为
的对数, 记为![]() (即
(即![]() ) .如
) .如![]() , 则4叫做以3为底81的对数, 记为
, 则4叫做以3为底81的对数, 记为![]() (即
(即![]() ) .
) .
(1)计算下列各对数的值:![]() ;
;![]() ;
;![]() .
.
(2)观察(1)中三数4、16、64之间满足怎样的关系式,![]() 之间又满足怎样的关系式;
之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
(4) 根据幂的运算法则:![]() 以及对数的含义说明上述结论.
以及对数的含义说明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 、
、![]() 在坐标轴上,
在坐标轴上, ![]() 是
是![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的,点
得到的,点![]() 在
在![]() 轴上,直线
轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,线段
,线段![]() ,
,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,平面内是否存在点
轴上,平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请直接写出点
为顶点的四边形是矩形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=α.∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠A2019BC与∠A2019CD的平分线相交于点A2020,得∠A2020,则∠A2020=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点。现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为________
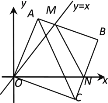
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有______________
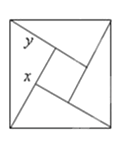
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com