
 如图,已知⊙O的半径为4,弦BC长为4
如图,已知⊙O的半径为4,弦BC长为4| 3 |
| 3 |
| OD |
| OB |
| 1 |
| 2 |
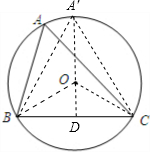 解:如图,连接OB、OC;过点O作OD⊥BC;
解:如图,连接OB、OC;过点O作OD⊥BC;| 3 |
| OD |
| OB |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 7 |
| 5 |
| 8 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、21.96 |
| B、2196 |
| C、219.6 |
| D、0.2196 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,小明开着汽车在公路上行驶到A处时,高塔B在A的北偏东60°方向上,小明以每分钟125米的速度向东行驶,到达C处时,高塔B在C的北偏东30°方向上,到达D处时,高塔B在D的北偏西30°方向上,当汽车到达D处时恰与高塔B相距500米.
如图所示,小明开着汽车在公路上行驶到A处时,高塔B在A的北偏东60°方向上,小明以每分钟125米的速度向东行驶,到达C处时,高塔B在C的北偏东30°方向上,到达D处时,高塔B在D的北偏西30°方向上,当汽车到达D处时恰与高塔B相距500米.查看答案和解析>>
科目:初中数学 来源: 题型:
 用一副等腰直角三角板和30°的直角三角板拼成如图所示的图形,其中∠BAD=90°,AB=AD,∠DBE=30°,∠DEB=90°,连接AE,求∠AEB的度数.
用一副等腰直角三角板和30°的直角三角板拼成如图所示的图形,其中∠BAD=90°,AB=AD,∠DBE=30°,∠DEB=90°,连接AE,求∠AEB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
 甲乙两人在同一条笔直的公路上步行从A地去往B地,已知甲乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离y(千米)与甲步行的时间t(小时)的函数关系图象如图所示,下列说法①乙的速度为2千米/小时;②乙到终点时甲乙相距9千米;③当乙追上甲时,两人距A地21千米;④A,B两地距离为27千米.其中正确的个数为( )
甲乙两人在同一条笔直的公路上步行从A地去往B地,已知甲乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离y(千米)与甲步行的时间t(小时)的函数关系图象如图所示,下列说法①乙的速度为2千米/小时;②乙到终点时甲乙相距9千米;③当乙追上甲时,两人距A地21千米;④A,B两地距离为27千米.其中正确的个数为( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com