
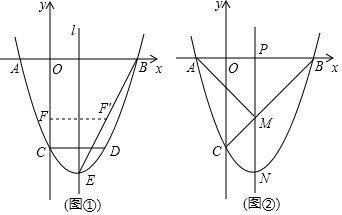
分析 (1)由条件可求得抛物线对称轴,则可求得b的值;由OB=OC,可用c表示出B点坐标,代入抛物线解析式可求得c的值;
(2)可设F(0,m),则可表示出F′的坐标,由B、E的坐标可求得直线BE的解析式,把F′坐标代入直线BE解析式可得到关于m的方程,可求得F点的坐标;
(3)设点P坐标为(n,0),可表示出PA、PB、PN的长,作QR⊥PN,垂足为R,则可求得QR的长,用n可表示出Q、R、N的坐标,在Rt△QRN中,由勾股定理可得到关于n的二次函数,利用二次函数的性质可知其取得最小值时n的值,则可求得Q点的坐标,
解答 解:
(1)∵CD∥x轴,CD=2,
∴抛物线对称轴为x=1.
∴$-\frac{b}{2}=1,b=-2$.
∵OB=OC,C(0,c),
∴B点的坐标为(-c,0),
∴0=c2+2c+c,解得c=-3或c=0(舍去),
∴c=-3;
(2)设点F的坐标为(0,m).
∵对称轴为直线x=1,
∴点F关于直线l的对称点F的坐标为(2,m).
由(1)可知抛物线解析式为y=x2-2x-3=(x-1)2-4,
∴E(1,-4),
∵直线BE经过点B(3,0),E(1,-4),
∴利用待定系数法可得直线BE的表达式为y=2x-6.
∵点F在BE上,
∴m=2×2-6=-2,即点F的坐标为(0,-2);
(3)存在点Q满足题意.
设点P坐标为(n,0),则PA=n+1,PB=PM=3-n,PN=-n2+2n+3.
作QR⊥PN,垂足为R,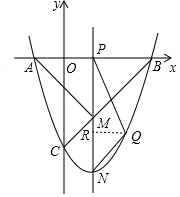
∵S△PQN=S△APM,
∴$\frac{1}{2}({n+1})({3-n})=\frac{1}{2}({-{n^2}+2n+3})•QR$,
∴QR=1.
①点Q在直线PN的左侧时,Q点的坐标为(n-1,n2-4n),R点的坐标为(n,n2-4n),N点的坐标为(n,n2-2n-3).
∴在Rt△QRN中,NQ2=1+(2n-3)2,
∴$n=\frac{3}{2}$时,NQ取最小值1.此时Q点的坐标为$({\frac{1}{2},-\frac{15}{4}})$;
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2-4).
同理,NQ2=1+(2n-1)2,
∴$n=\frac{1}{2}$时,NQ取最小值1.此时Q点的坐标为$({\frac{3}{2},-\frac{15}{4}})$.
综上可知存在满足题意的点Q,其坐标为$({\frac{1}{2},-\frac{15}{4}})$或$({\frac{3}{2},-\frac{15}{4}})$.
点评 本题为二次函数的综合应用,涉及待定系数法、轴对称、三角形的面积、勾股定理、二次函数的性质、方程思想及分类讨论思想等知识.在(1)中求得抛物线的对称轴是解题的关键,在(2)中用F点的坐标表示出F′的坐标是解题的关键,在(3)中求得QR的长,用勾股定理得到关于n的二次函数是解题的关键.本题考查知识点较多,综合性较强,特别是最后一问,难度很大.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
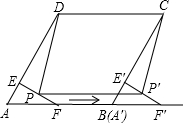 如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A'E'F'.设 P、P'分别是 EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )
如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A'E'F'.设 P、P'分别是 EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )| A. | 28$\sqrt{3}$ | B. | 24$\sqrt{3}$ | C. | 32$\sqrt{3}$ | D. | 32$\sqrt{3}$-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2m的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是1m2.
如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2m的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是1m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
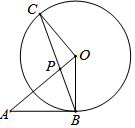 如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8岁 | B. | 9岁 | C. | 10岁 | D. | 11岁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com