
 七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那副图是( )
七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那副图是( )| A. | 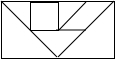 | B. |  | ||
| C. |  | D. | 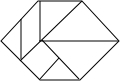 |
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
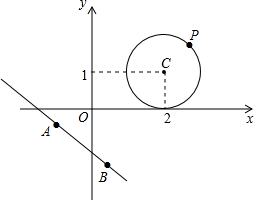 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
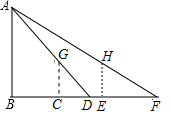 小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.7米,求路灯杆AB的高度.
小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.7米,求路灯杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com