练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，点P(1，4)，Q(m，n)在函数y＝ (x＞0)的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C，D.QD交PA于点E，随着m的增大，四边形ACQE的面积(　　)

    A. 减小 B. 增大 C. 先减小后增大 D. 先增大后减小

    【答案】B

    【解析】解：AC=m﹣1，CQ=n，则S四边形ACQE=ACCQ=（m﹣1）n=mn﹣n．

    ∵P（1，4）、Q（m，n）在函数（x＞0）的图象上，∴mn=k=4（常数），∴S四边形ACQE=ACCQ=4﹣n，∵当m＞1时，n随m的增大而减小，∴S四边形ACQE=4﹣n随m的增大而增大．故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图， ABC的中线AD、BE相交于点F，下列结论正确的有 （ ）

    ①S△ABD=S△DCA；② S△AEF=S△BDF；③S四边形EFDC=2S△AEF；④S△ABC=3S△ABF

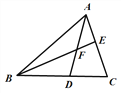
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠A=60°，BE⊥AC，垂足为E，CF⊥AB，垂足为F，点D是BC的中点，BE，CF交于点M．

    （1）如果AB=AC，求证：△DEF是等边三角形；

    （2）如果AB≠AC，试猜想△DEF是不是等边三角形？如果△DEF是等边三角形，请加以证明；如果△DEF不是等边三角形，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为提高饮水质量，越来越多的居民开始选购家用净水器．一商家抓住商机，从厂家购进了A、B两种型号家用净水器共160台，A型号家用净水器进价是150元/台，B型号家用净水器进价是350元/台，购进两种型号的家用净水器共用去36000元．

    （1）求A、B两种型号家用净水器各购进了多少台；

    （2）为使每台B型号家用净水器的毛利润是A型号的2倍，且保证售完这160台家用净水器的毛利润不低于11000元，求每台A型号家用净水器的售价至少是多少元？（注：毛利润=售价﹣进价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，D、E分别在边AB、AC上，DE∥BC．

    （1）试问△ADE是否是等腰三角形，并说明理由.

    （2）若M为DE上的点，且BM平分，CM平分，若的周长为20，BC=8.求的周长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，过点M(－3，2)分别作x轴、y轴的垂线与反比例函数y＝的图象交于A，B两点，则四边形MAOB的面积为____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形ABCD中，AD∥BC，AP平分∠DAB，BP平分∠ABC，它们的交点P在线段CD上，下面的结论：①AP⊥BP；②点P到直线AD，BC的距离相等；③PD＝PC.其中正确的结论有( )

    A. ①②③ B. ①② C. ① D. ②

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分．前6名选手的得分如下：

    　　　　序号

    项目

    1

    2

    3

    4

    5

    6

    笔试成绩/分

    85

    92

    84

    90

    84

    80

    面试成绩/分

    90

    88

    86

    90

    80

    85

    根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)．

    （1）这6名选手笔试成绩的中位数是________分，众数是________分；

    （2）现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比；

    （3）求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线OM⊥ON，垂足为O，三角板的直角顶点C落在∠MON的内部，三角板的另两条直角边分别与ON、OM交于点D和点B．

    （1）填空：∠OBC+∠ODC=　 　；

    （2）如图1：若DE平分∠ODC，BF平分∠CBM，求证：DE⊥BF：

    （3）如图2：若BF、DG分别平分∠OBC、∠ODC的外角，判断BF与DG的位置关系，并说明理由。

    查看答案和解析>>

    同步练习册答案