Question

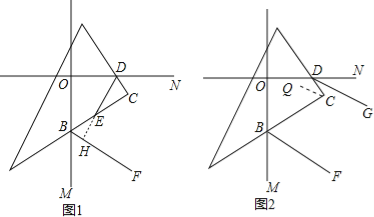
【题目】如图，直线OM⊥ON，垂足为O，三角板的直角顶点C落在∠MON的内部，三角板的另两条直角边分别与ON、OM交于点D和点B．

（1）填空：∠OBC+∠ODC=　 　；

（2）如图1：若DE平分∠ODC，BF平分∠CBM，求证：DE⊥BF：

（3）如图2：若BF、DG分别平分∠OBC、∠ODC的外角，判断BF与DG的位置关系，并说明理由。

Answer 1

【答案】（1）180°；（2）见解析；（3）BF∥DG．

【解析】试题分析：（1）先利用垂直定义得到∠MON=90°，然后利用四边形内角和求解；

（2）延长DE交BF于H，如图，由于∠OBC+∠ODC=180°，∠OBC+∠CBM=180°，根据等角的补角相等得到∠ODC=∠CBM，由于DE平分∠ODC，BF平分∠CBM，则∠CDE=∠FBE，然后根据三角形内角和可得∠BHE=∠C=90°，于是DE⊥BF；

（3）作CQ∥BF，如图2，由于∠OBC+∠ODC=180°，则∠CBM+∠NDC=180°，再利用BF、DG分别平分∠OBC、∠ODC的外角，则∠GDC+∠FBC=90°，根据平行线的性质，由CQ∥BF得∠FBC=∠BCQ，加上∠BCQ+∠DCQ=90°，则∠DCQ=∠GDC，于是可判断CQ∥GD，所以BF∥DG．

（1）解：∵OM⊥ON，

∴∠MON=90°，

在四边形OBCD中，∠C=∠BOD=90°，

∴∠OBC+∠ODC=360°﹣90°﹣90°=180°；

故答案为180°；

（2）证明：延长DE交BF于H，如图1，

∵∠OBC+∠ODC=180°，

而∠OBC+∠CBM=180°，

∴∠ODC=∠CBM，

∵DE平分∠ODC，BF平分∠CBM，

∴∠CDE=∠FBE，

而∠DEC=∠BEH，

∴∠BHE=∠C=90°，

∴DE⊥BF；

（3）解：DG∥BF．理由如下：

作CQ∥BF，如图2，

∵∠OBC+∠ODC=180°，

∴∠CBM+∠NDC=180°，

∵BF、DG分别平分∠OBC、∠ODC的外角，

∴∠GDC+∠FBC=90°，

∵CQ∥BF，

∴∠FBC=∠BCQ，

而∠BCQ+∠DCQ=90°，

∴∠DCQ=∠GDC，

∴CQ∥GD，

∴BF∥DG．