
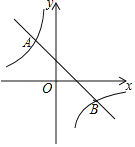
【题目】如图,一次函数y1=kx+2图象与反比例函数y2=![]() 图象相交于A,B两点,已知点B的坐标为(3,﹣1).
图象相交于A,B两点,已知点B的坐标为(3,﹣1).
(1)求一次函数和反比例函数的解析式;
(2)请直接写出不等式kx﹣![]() ≤﹣2的解集;
≤﹣2的解集;
(3)点C为x轴上一动点,当S△ABC=3时,求点C的坐标.
【答案】(1)y1=﹣x+2,y2=![]() ;(2)﹣1≤x<0或x≥3;(3)(
;(2)﹣1≤x<0或x≥3;(3)(![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)将B的坐标(3,﹣1)分别代入一次函数y1=kx+2图象与反比例函数y2=![]() 中,可求出k、m的值,进而确定函数关系式,
中,可求出k、m的值,进而确定函数关系式,
(2)求出一次函数与反比例函数图象的交点坐标,根据图象得出不等式的解集,
(3)求出一次函数与x轴的交点坐标,根据S△ABC=3,可以求出CM的长,分两种情况进行解答即可.
解:(1)把B(3,﹣1)分别代入y1=kx+2和y2=![]() 得:
得:
﹣1=3k+2,m=3×(﹣1),
∴k=﹣1,m=﹣3,
∴一次函数和反比例函数的解析式分别为y1=﹣x+2,y2=![]() ,
,
(2)由题意得:
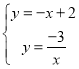 ,解得:
,解得: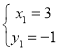 ,
, ,
,
∴A(﹣1,3)
不等式kx﹣![]() ≤﹣2的解集,即kx+2≤
≤﹣2的解集,即kx+2≤![]() 的解集,由图象可得,﹣1≤x<0或x≥3,
的解集,由图象可得,﹣1≤x<0或x≥3,
∴不等式kx﹣![]() ≤﹣2的解集为﹣1≤x<0或x≥3.
≤﹣2的解集为﹣1≤x<0或x≥3.
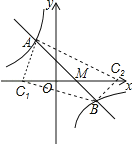
(3)直线y=﹣x+2与x轴的交点M(2,0),即OM=2,
∵S△ABC=3,
∴S△AMC+S△BMC=3
即:![]() ×CM×3+
×CM×3+![]() CM×1=3,
CM×1=3,
解得:CM=![]() ,
,
①当点C在M的左侧时,OC1=2﹣![]() =
=![]() ,
,
∴点C的坐标为(![]() ,0),
,0),
②当点C在M的右侧时,OC2=2+![]() =
=![]() ,
,
∴点C的坐标为(![]() ,0),
,0),
综合上述,点C的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】下列函数中,自变量的取值范围选取错误的是
A.y=2x2中,x取全体实数
B.y=![]() 中,x取x≠-1的实数
中,x取x≠-1的实数
C.y=![]() 中,x取x≥2的实数
中,x取x≥2的实数
D.y=![]() 中,x取x≥-3的实数
中,x取x≥-3的实数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔![]() 的高度,他从点
的高度,他从点![]() 处的观景塔出来走到点
处的观景塔出来走到点![]() 处.沿着斜坡
处.沿着斜坡![]() 从
从![]() 点走了
点走了![]() 米到达
米到达![]() 点,此时回望观景塔,更显气势宏伟.在
点,此时回望观景塔,更显气势宏伟.在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 且
且![]() ,再往前走到
,再往前走到![]() 处,观察到观景塔顶端的仰角
处,观察到观景塔顶端的仰角![]() ,测得
,测得![]() 之间的水平距离
之间的水平距离![]() 米,则观景塔的高度
米,则观景塔的高度![]() 约为( ) 米. (
约为( ) 米. (![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
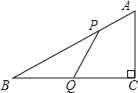
【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在等边三角形![]() 中,
中,![]() 是
是![]() 边上的动点,以
边上的动点,以![]() 为一边,向上作等边三角形
为一边,向上作等边三角形![]() ,连接
,连接![]() .
.
(1)![]() 和
和![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)试说明:![]() ;
;
(3)如图(2),将动点![]() 运动到边
运动到边![]() 的延长线上,所作三角形
的延长线上,所作三角形![]() 仍为等边三角形,请问是否仍有
仍为等边三角形,请问是否仍有![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB垂直弦CD于点E,点F在AB的延长线上,且∠BCF=∠A.
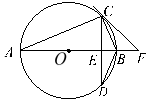
(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sin∠D的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将![]() 经过一次平移后得到
经过一次平移后得到![]() ,图中标出了点
,图中标出了点![]() 的对应点
的对应点![]() .(小正方形边长为1,
.(小正方形边长为1,![]() 的顶点均为小正方形的顶点)
的顶点均为小正方形的顶点)
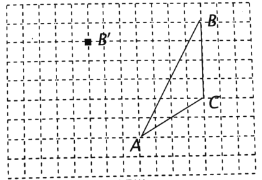
(1)补全![]() ;
;
(2)画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 中
中![]() 边上的高线
边上的高线![]() ;
;
(4)![]() 的面积为_____.
的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(﹣1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
①4a+b=0;
②9a+3b+c<0;
③若点A(﹣3,y1),点B(﹣![]() ,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
④若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 .
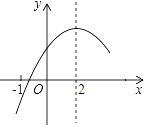
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com