
【题目】如图,⊙O的直径AB垂直弦CD于点E,点F在AB的延长线上,且∠BCF=∠A.
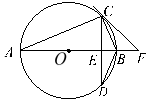
(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sin∠D的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,由OA=OA可知∠ACO=∠A,再根据∠FCB=∠A可知∠ACO=∠FCB,由于AB是⊙O的直径,所以∠ACO+∠OCB=90°故∠FCB+∠OCB=90°故可得出结论;
(2)由AB是⊙O的直径,CD⊥AB可知
试题解析: (1)连接OC,
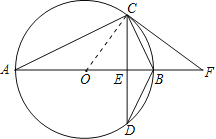
∵OA=OC,
∴∠ACO=∠A,
又∵∠FCB=∠A
∴∠ACO=∠FCB,
又∵AB是⊙O的直径
∴∠ACO+∠OCB=90°,∠FCB+∠OCB=90°
∴直线CF为⊙O的切线,
(2)∵AB是⊙O 直径
∴∠ACB=90°
∵DC⊥AB
∴![]()
∴BC=BD,∠A=∠D
∴![]()
考点: 1.切线的判定;2.圆周角定理;3.解直角三角形.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在航线![]() 的两侧分别有观测点A和B,点A到航线
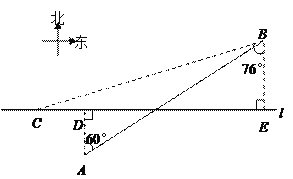
的两侧分别有观测点A和B,点A到航线![]() 的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.
的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.
(1)求观测点B到航线![]() 的距离;
的距离;
(2)求该轮船航行的速度(结果精确到0.1km/h).(参考数据: ![]() 1.73,sin76°≈0.97,cos≈0.24,tan76°≈0.4.01)
1.73,sin76°≈0.97,cos≈0.24,tan76°≈0.4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列出下列问题中的函数关系式,并判断它们是否为反比例函数.
(1)某农场的粮食总产量为1 500t,则该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,则总价y(元)与加油量x(L)的函数关系式;
(3)小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
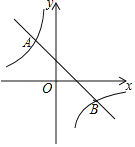
【题目】如图,一次函数y1=kx+2图象与反比例函数y2=![]() 图象相交于A,B两点,已知点B的坐标为(3,﹣1).
图象相交于A,B两点,已知点B的坐标为(3,﹣1).
(1)求一次函数和反比例函数的解析式;
(2)请直接写出不等式kx﹣![]() ≤﹣2的解集;
≤﹣2的解集;
(3)点C为x轴上一动点,当S△ABC=3时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为﹣4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(﹣1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
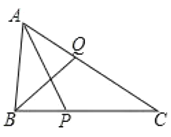
【题目】如图,在△ABC中,∠BAC=60°,∠C=40°,P,Q分别在BC,CA上,AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为∠CAF的角平分线,BD=CD,∠DBC=∠DCB,∠DCA=∠ABD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD中,∠ACB=∠ECD=a,且AC=BC,EC=DC,AE、BD交于P点,连CP
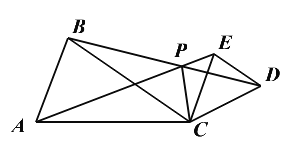
(1)求证:△ACE≌△BCD
(2)求∠APC的度数(用含a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
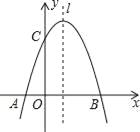
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com